この本を，今の時代に読む人はいないだろうなと思いつつ，ちょっと開いてみました。
算数ソフトを作る時に使っているソフトが，ディレクターです。バージョンが１１．５まで進んでいます。
この本は，ディレクターのバージョン８の時代の参考書です。非常に詳しい本で，ある程度の水準にある人には，手放せない本です。
たまたま，開いたところが３Ｄのサンプルについて解説していたところでした。そこを良く読むと，どうも，パラメーターの設置ができるようなことが書いてあります。具体的にどういう事か気になり，サンプルソフトを開いてみました。
ところが，サンプルソフトのバージョンが古いために，開くためにはディレクター独特のバックアップ作業を要します。
それをちょちょいとやって，開いてみたら，これがとても勉強になりました。
パラメーターが作れたからと言って，作る作品に変化が起こるわけではありません。
作る過程が，ちょっと変化する感じです。
算数・数学的に言えば，文章問題を見て，未知数をＸにして方程式で解いていくようなものです。具体的に考えて解くこともできますが，式が複雑になるので，修正がちょっと大変なのです。
そんな感触を受けています。
良い感触なのですが，これが身につくかどうかは，疑問です。
まずは，何をパラメーターとしたいか，そういった全体を見通す力量が必要に思えています。私のように，思いついたことをどんどん作り進め，後から，気に入らないところを直すというやり方では，ちょっとパラメーターは使いこなせないかもしれません。これも，やってみなければ分かりませんので，今作っている作品が完成したら，その次からちょっとチャレンジしてみようと思います。
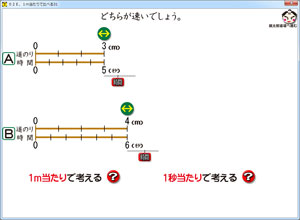今作っているのは，６年の速さのソフトです。
道のりと時間を決めて，それを１ｍ当たり，１秒当たりで比べる勉強ができるソフトです。
まだ，もう少し，作り込む必要があるので，少々時間がかかっています。新年には，もっと算数サイトにアップできると思います。
この作品も良い感じの作品になりそうで，目下，気に入っています！
学期末に，算数ソフトを使って大盛り上がりをしたと教えてくれたのは，関西の関田先生です。
この日曜日に，関田先生が事務局となって野口塾が開催されます。そこで，私も「算数で作法」をお話ししてきます。
算数の時間に作法を指導しましょう！という，ちょっと変わった講座ですが，算数ソフトを使っている先生でしたら，至極，当然と感じているはずです。
ソフトを使うと，子ども達のやる気が非常に高まります。
しかも，連日，この高いやる気が持続します。
やる気が高い状態というのは，勉強そのものが面白いだけでなく，先生のことが大好きになっている状態です。大好きな先生が，こんな風なクラスが良いなぁ，と思うことを子ども達に話しをしたら，その方向に子ども達は流れを作ってくれます。
そこから，各種作法がクラスの形として，次第に安定的に保たれるようになると，クラスは「立派ですね」と思われる方向に変わっていきます。
神戸では作法で３０分，算数ソフトで３０分ぐらい話しをする予定です。
「奇跡の算数セミナー」で，関田先生とあまりお話しできなかったので，この日はいろいろと話しをしたいと思っています。
５年生で学習する「帯グラフ・円グラフ」
この単元で算数ソフトを使っている渥美先生から，とってもうれしいメールをいただきました。
－－－－－－－－－－－－
言いたくて仕方が無くなる。
聞きたくて仕方が無くなる。
こういう状態になります。
－－－－－－－－－－－－
マウスでクリックしていると，子ども達が「言いたくて仕方がない状態」になるのです。
答えも言いたいし，どうしてなのかも言いたいし・・・
そんな嬉しい状態になるのです。
普通の授業では，いつも決まった子ばかりが手を挙げがちです。
時々，違う子が手を挙げると，その子を優先して・・・・。
あの子にもこの子にも，もっと手を挙げて欲しいあぁ・・・と思います。
そういう状態が，算数ソフトを使うと一変します。
子ども達がやる気満々になってくれるので，先生の話もとても良く聞いてくれます。
「もっと知りたい！」という気持ちになっていきます。
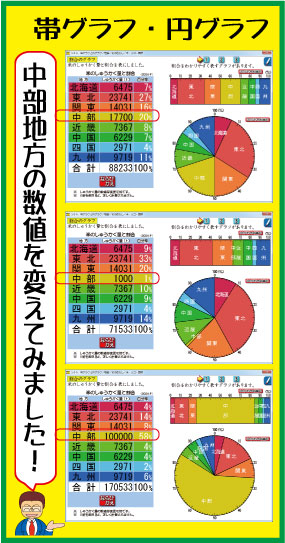例えば，ソフトの中の中部地方の数値をちょこっと変えてみます。
何も変えないときの中部地方は「１７７００ｔ」。黄土色のところです。順位は第２位。
この数値を，わざと「１０００ｔ」に減らしてみます。
すると，どうなるでしょう。割合は１％ですから，帯グラフも円グラフも狭くなります。順位はビリです。
今度は，「１０万ｔ」に増やしてみます。
すると，５８％にもなります。中部地方のグラフは広くなり，順位は１位へと変わります。
こんな風に２回，３回と変更してみて，それから子ども達の希望に合わせて，１つの地方の数値を変更したら，どうなるでしょう。
「広くなる！」「狭くなる！」
「○○地方と同じぐらいになる！」
「○○地方の２倍ぐらいになる！」
あれこれ，言いたくなりますよね。
人間は不思議な生き物で，ある程度の理解が進むと，そのことについて言いたくなってきます。
「ある程度の理解」に達する前だと，妙に口ごもります。わざと知らない振りをすることもあります。
それが，ちょっと分かってくると，気持ちが動き始めます。
かなり知った状態になると，一言も二言も言いたくなります。人によっては，つい口走ることすらあります。
学習の大事なポイントは，この「ある程度の理解が進む」状態にまで，トントンと進めることです。それには，２回，３回とやってみせることです。
繰り返されると，そこにきまりが見えてくるので，あれこれ見えてきて，次第に言いたくなってくるのです。
ここを１回目から考えさせようとすると，頭が動きにくくなります。授業も重くなりますね。
－－
このソフトは，『子どもが夢中で手を挙げる算数の授業』の５年２巻に入っています。
６年生の「速さ」。
この単元の基本といえば，５０ｍを８秒で走ったとか，４０ｍを７秒で走ったという記録です。
この単元は，「単位量当たり」という考え方の流れを汲んでいるので，これを普通は「１秒当たり」の秒速で比べます。でも，考える力を高めるためたい場合には，「１ｍ当たり」で比べることもできることを学んだ方が良いです。
「１秒当たり」「１ｍ当たり」。
この両方の見方を分かりやすく表現するときに，役立つのが線分図です。
でも，どうやったら，その「分かりやすさ」を示せるのでしょう。それが頭の使い所です。
私の雰囲気ですと，道のりの方から動き出すのが「１ｍ当たり」。時間の方から動き出すのが「１秒当たり」という感じにすると，少し分かりやすくなるかなと思っています。
でも，こういうのは，実際に付くって動かしてみないと感触がわかりません。
今週中には作り進めて，現状の言葉で理解する状態よりは１歩も２歩も分かりやすいソフトに仕上げたいと思っています。
ところで，「速さ」という概念ですが，これを考えついたのは，万有引力で有名なあのニュートンです。時間と空間を結びつけて考えたのです。ニュートンは算数・数学でも偉人です。
「チーム・奇跡の算数」の続き。
中田先生から，５年生の「図形の面積」の指導案が提案されました。
よく考えられていて，この授業なら子ども達の頭はフル回転すると感じました。特に，導入は興味をかき立てる形になっていて，上手いなと思いました。
中田先生の授業でもソフトが使われました。そのソフトは，教室プレゼンターを使って算数ソフトを開発し続けている種市先生が作られたものです。いつかはお会いしたいと思っている先生のお名前が出て，とても身近に感じられました。
学校の先生をやりながらソフトを開発するのはとても大変です。特に，マウスドラッグで図形を動かすのは，なかなか面倒で手間がかかります。 そこが作り進められないと伺ったので，私の方でも作ってみることにしました。
中田先生とのコラボソフトです。
右をご覧の通り，三角形の頂点をドラッグして，頂点を動かすことができます。
これが，「等積変形」です。面積を変えずに形だけを変えることです。
大切な概念なので，面積の授業では子ども達にしっかり見せたいのですが，思うように見せられないところとなっています。
面積を保存したまま，形を変えるのが「等積変形」。
これと同等に大切な見方があります。形を保存したまま，位置を変える「等積移動」です。
等積移動には，「平行移動」「回転移動」があります。
このソフトには，「回転移動」の機能も付けています。
左下に小さな４つのボタンがあります。これが回転移動をスタートさせるボタンです。どんな風に回転するのでしょうか。ソフトがアップされましたら，ダウンロードしてご覧になって下さい。
このソフトを使って，白と水色の部分の面積が等しいことを学びます。
等積変形を何度も見て，回転移動で等しさの確認ができるように作られています。
ここまでつくってあると，見ている内に，等しくなる理由（言い換えれば，「等しくなることの論証」）を言いたくなってきます。教科書の画像を見ているだけではできない，質の高い授業ができます。
おまけの機能が付いています。
長方形の中のどこか好きなところをクリックすると，頂点がクリックしたところに瞬間移動します。好きなところをクリックすると，そこに頂点ができるのです。
これが，数学でよく登場する「任意の１点」をとる行為です。
任意の１点について，子ども達が「どこでも点」と言っていたことを中田先生が話してくれました。こういう重要なところを聞き逃さず大切に扱う所，さすがだと思いました。
数学用語を平易に言う言葉を，「辺」を「へり」，「頂点」を「かど」などのように，固定化することが学習として大切です。これから先，私は「任意の１点」を「どこでも点」として使っていきたいと思います。
★図形のソフトは，近日中に，もっと算数サイトにアップされます。
押田先生から，折り紙の実践が語られました。
私は算数で折り紙をあまり使ったことがないので，珍しさが先立ちました。
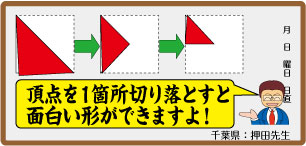先生の指示通りに，折り紙をおります。毎度，三角形になるように３回折り，そこにハサミを１回だけ入れます 。
開いてみると，これが何とも言えない形。
こういう遊びのようなことをしていると，やっていることを説明するために，意外と算数用語を使うことになります。
まずは，「三角」とか「三角形」が出てきます。
三角形になるように折っているのですから，どうしても口にせざるを得ません。
元が正方形の折り紙ですから，「四角」とか「正方形」とかも口に出やすいです。
折り紙ですから，「かどをそろえて」と出てきたら，それはもう「頂点」です。
「へりを合わせて」は「辺」ですし，「折り目」は「直線」「辺」。「真ん中」は「中心」ですよね。
子ども達が自然に使っている言葉を，意図的に算数用語に切り替えて先生が話し始めるだけで，「生活語」から「算数語」への大成長を促すことができます。
三角 →三角形
四角 →四角形
かど →頂点
線 →直線
真ん中→中心
へり →辺
押田先生は，紙の大きさを各種用意したので，「拡大」とか「縮小」という言葉も飛び交っていたそうです。
折り紙で楽しみながら，算数用語に慣れ親しんでいくこの実践。実に良いなと思いました。
こういう勉強の時，作った折り紙に，「用語を書き込む」ことがお勧めです。書き込みが成された折り紙を見ると，妙に勉強をしている感じがしてきます。
書き込んだ折り紙はノートに貼ります。そこだけ分厚くなるので，自然と開きやすくなり，その度に用語を目にすることになります。
みんなで実際に折り紙を折って，切って，なんだか楽しい一時でした。
