横田経一郎先生が，実に面白い本を出しています。
『教室マジック２４』（小学館）です。
この本には教室で簡単にできる手品が載っています。ＤＶＤには種明かしムービーが収録されています。
本を開いた時には，一つ一つの手品について，どれもこれも，どうやるのか全く分かりませんでした。
でも，ＤＶＤを見たら，これが実に簡単なんです。面白い！と感動しました。
この中の１つ２つを持ちネタにし，子ども達にやって見せたら，その瞬間から先生は特別な先生になってしまいそうです。
ＤＶＤの種明かしを見て思ったことは，横田先生のセンス良さです。数ある手品の中から，２４本を選ぶのですが，選ばれているマジックを見て，そのセンスの良さが出ます。教師としての腕も相当に高いと感じます。
実際，横田先生とは若い頃に一緒に勉強をしていましたが，その頃から暖かい感覚で子ども達を包むような優れた感性を持っている先生でした。ユーモアもあり，本も良く読んでいる，実力派の先生でしたので，彼が「いい！」と言うことは，たいてい「なるほど！」と頷いていました。このマジックも，まさに横田先生の教師としての眼力が光っています。お薦めします。
低学年の１２本のマジックの中に，割り箸のマジックあるのですが，今，これが私のお気に入りです。
小学校で習うグラフは，昨年度までは次の４つでした。
棒グラフ
折れ線グラフ
帯グラフ
円グラフ
これに，新しく今年度から次のグラフが登場します。
柱状グラフ
昔の算数に登場していた「柱状グラフ」が帰ってきたのです。
合計５つのグラフを学ぶのですが，それぞれの特徴をざっくりと把握していると，指導の味が少し変わってきます。
棒グラフは，多い少ないがわかりやすいグラフです。
折れ線グラフは，変化がわかりやすいグラフです。
帯・円グラフは，全体のどれくらいかという割合がわかりやすいグラフです。
そうして，柱状グラフです。
これは，いったい何がわかりやすいのでしょう。
こういうグラフの特徴がわかると，調べたことをグラフ化する時，どのグラフで表したら効果的かがわかります。伝わりやすい「見せ方」ができるのです。
たとえば，「お小遣い」をテーマにしても，どのグラフが良いか，状況によって決まってきます。
友達との違いを見るなら，棒グラフです。
小さいときからのお小遣いの推移なら，折れ線グラフです。
今月のお小遣いを何にどれだけ使ったかなら，帯や円グラフです。
グラフ選びは，伝え方技術の一つなのです。
小学校の授業では，グラフを選んで伝え方を考える所まで進みませんが，社会などとの関連でグラフ化したい時に，こういった算数の考えが役に立ちます。
柱状グラフ。これは，「さくら算数ソフト」６年５巻に入っています。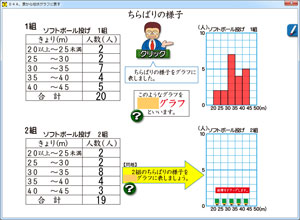
右のソフトは，表から柱状グラフに変換するところを学ぶソフトです。上の表とグラフがお手本で，下は実際にマウス操作で柱状グラフの「柱」づくりが出来るようになっています。
もちろん，クリックすれば，何回でも繰り返し勉強できます。
柱状グラフで難しいのは，柱の「範囲」にどのデータが入るか，というところです。そこの所もソフトには収録されているので，動きを見れば，「なるほど！」がやってきます。
一つ一つの柱に入っている人数を高さで示すことで，「分布」が分かりやすくなります。身近なところでは，テストの点数も，１０点刻みで範囲をもうけ，その中に何人はいるかを柱状グラフにすると，そのテストの傾向が見えてきます。
グラフとして学ぶのは５種類なのですが，実は，数直線もグラフの一種です。文章問題に出てくるテープ図や線分図もグラフの一種といえます。数を配置することで，見えやすく，わかりやすくしているのです。テープ図や線分図を文章題で用いるのは，数を配置することにより，どういう計算になるかを考える思考の場所にしているのです。このあたりのことについては，文章題の話題の折りに書いていきます。
日常の指導も，グラフのように「見える」ようにすることで，伝わりが良くなります。
「あなたの話の中身が見えてきた」「君の話はよく見えない」という言葉から始まっているのが左の山本正実先生の『伝わる伝わる見える指導』です。
指導のキーワードは「見える」
具体的な物とつながると「見える」
指導力も伸ばす「見える」指導
と，グッと来る話が書いてあります。
私が算数のソフトを作り続けているのも，この「見える」の考え方の流れに乗っています。
ソフトでは，算数の動きが「見える」から，伝わる指導になるのです。
工作用紙で箱を作って，その容積を考えるソフトです。
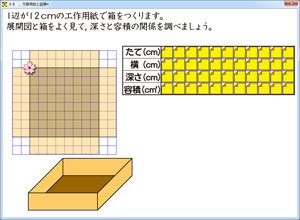
展開図の切り口の所に桜スライダーがセットしてあります。
「さくら算数ソフト」を御愛用の先生には，もうピンと来ていると思います。
この桜スライダーを動かすと，もしかして，展開図の底面が狭くなったり，広くなったりするのでは？？？
まさに，その通りです。
そればかりでなく，その下にある箱の底面・側面のサイズも，展開図に合わせて変化します。
こういう「連動」を見るだけでも，算数の面白さが伝わります。
紙サイズが一定なので，底面の縦横が短くなると，側面の高さが高くなる。
こういう「縦横高さ」の関係が見て取れます。しかも，方眼がついているので，数値を意識して考えることも出来ます。十分に算数的です。
でも，容積と深さとは，正比例・反比例といった関係にはなりません。どんな風な関係になっているのでしょうか。表を見ても余りよくつかめません。関係をつかむには，グラフが一番です。変化の様子が見て直ぐにわかるからです。今風に言えば，「グラフは数値の見える化」なのです。だから，わかりやすく，把握しやすいのです。
そのグラフを作り込んだら，完成します。
明日には完成させて，近日中にアップしたいと思います。
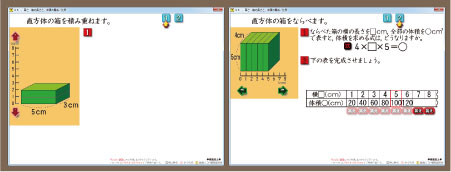
体積を使って，「比例」の学習を少しします。
「比例」は，中学の「関数」になる勉強です。折に触れて，ちょこっと勉強しておくことはとても大切です。
２問用意しました。
すでに，「２つの数の変わり方」の学習を４年生でしています。また，体積のメインの学習から外れます。ですので，１問やれば十分という気がします。でも，それではちょっと！と思ってしまうのが，教師経験者の思いです。
１問目が終わってようやく思い出す子がいるからです。エンジンのかかりが遅い子です。その子のためにもう一問取り組むことが大切と思っています。
算数ソフトですので，もう一問も，クリック一つで簡単にできます。上の画面の左側が１問目。右側が２問目です。直方体の向きが変わり，重なる方向が変わっています。それでも，「関数」は似たような感じになります。ですので，２問目を出したときに，出遅れ気味の子に活躍の場を与えてもらえたら，私はとっても嬉しいです！！
このソフトも，近日中にアップします。お楽しみに！
もうすぐ，ＧＷですね。「さくら算数ソフト」（さくら社の算数ソフト）を使っている先生は，ＧＷの谷間に算数の授業を展開することになっても，楽しめますよ。
なにしろ，「さくら算数ソフト」はきめ細かく作ってあるので，「復習に最適！」という声をいただいています。「学期末テストの前に，ざっとソフトを見て復習」，「年度末にソフトで総復習」。こういう使い方も効果的なのです。子ども達の思い出しが良いからです。
これをＧＷの谷間や，ＧＷ明けにぜひ体験してみてください。たぶん，どこかの単元の途中でＧＷに入ると思います。ＧＷ明けは，その単元の習ったところまでのソフトを見せてから，本時の学習に入りましょう。きっと，エンジンのかかりが良くなりますよ！
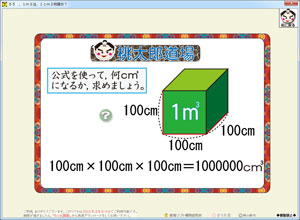「１００ｃｍ×１００ｃｍ×１００ｃｍ＝１００００００ｃｍ３」という式の意味がちょっとわかりやすくなるように作る予定です。
－－－－
昨日，このように書きました。そのソフトは，もうアップされています。ダウンロードされた先生は，「桃太郎道場」の所も見ていると思います。
良い感じに動きを出しました。
この動きをソフトで見せて，盛り上がったら，工作用紙で，似たような動きを演出できる教具を自作することをお薦めします。
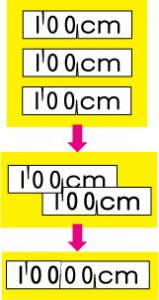「１００ｃｍ」と書いた工作用紙を３枚作ります。
そこに切れ目を入れます。ｃｍが隠れるように３枚組み合わせると，１０００００ｃｍとなります。
ちょっとした手品のようで，なかなか面白いです。
この教具の優れている点は，組み合わせた後，再び分けることが出来るので，授業の流れに応じて，つなげたりバラしたり出来ます。
ああ，でも，気がつきましたね。
単位が最後まで「ｃｍ」のままです。こういう重要なところで，工夫が簡単にできそうな所は，自分で作ってはいけません。子ども達に考えさせるのです。２枚で「２」，３枚で「３」を出す，子どもらしい方法を見つけてくれます。
そのアイデアに子どもの名前をつけて楽しむと，何倍も楽しめますね。
算数ソフトでわかりやすい授業を展開したら，ソフトの動きをヒントに，ちょっとした教具を作ってみるのも，算数を楽しくする，一つの新しい方法です。
明日には，もう１本，体積のソフトをアップする予定です。どうぞ，ごきたいください！！
※ ソフトを使って，嬉しい成果・効果などありましたら，横山までご一報ください。
http://www.kennya.jp/toiawase/
このブログなどでご紹介し，たくさんの先生方と喜びを分かち合いたいと思っています。
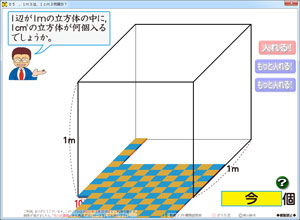１ｍ３の立方体の中に，１ｃｍ３の立方体が何個はいるか？
それを見て勉強するソフトです。
４年生の面積で，１ｍ２は１００００ｃｍ２と勉強したとき，紙を貼り付けて「確かに１万個ある！」と勉強します。操作学習といわれるタイプの勉強で，「経験すれば頭にはいる」と考える方法です。でも，私の経験からは，実際に作業をさせても，「１ｍ２＝１００００ｃｍ２」とスパッとわからない子がけっこういて，作業すれば良いってもんじゃない！と思っていました。
作業の弱点は，作業の中に数が表示されないことです。数を表示できるように，作業中の工夫をすれば，頭への入り方は変わってきます。
とはいっても，１ｍ３です。４年の時と同じように１ｃｍ３を積み重ねて・・・と言うわけにはいきません。何しろ，１００万個も使うからです。作業するだけで，何時間もかかってしまいます。
ですので，通常は１ｍ３の骨組みを作って，１ｍ３の大きさ（かさ）を体感してもらうように授業が進みます。当然，１００万個は，「１００×１００×１００」の計算でわかってもらうことになります。ここが，今の算数のちょっとした弱点です。
そこを補えたらと思い，目下，ソフトを開発中です！！
４年の面積で，「いよーっ！ いよーっ！」と歌舞伎声のする中，１ｃｍ２がどんどん出てきたあのソフトの兄貴分に当たるソフトです。見ているだけで楽しく，「確かに，１ｃｍ３がたっくさんある！」と感じます。
途中途中で今何個あるのかの確認が取れるように作っています。
これが，重要なのです。増えていくのをただ見ているだけでは，算数になりません。そこに「数が同時に表示される」ことが必要です。または，上の画像のような数を意識できる表し方（市松模様など）が必要です。数の同時表示により，動きを算数として見ることが出来るようになるからです。
そうして，このソフトに，「桃太郎道場」をこれから作り込みます。
「１００ｃｍ×１００ｃｍ×１００ｃｍ＝１００００００ｃｍ３」という式の意味がちょっとわかりやすくなるように作る予定です。
どうしたらわかりやすくなのでしょう。皆さんもちょっと考えてみてください。浮かんできた考えを，教具にして，授業してみてください。伝わりが少し良くなりますよ。
このソフト，明日には完成し，明後日にはアップできる予定です。
ソフトで１ｍ３の体験をしたら後，算数資料室から古い１ｍの竹尺を１２本持ってきて，１ｍ３の立体を作りましょう。楽しい授業になりますね。
