 平面図形の位置を見つけるソフトです。
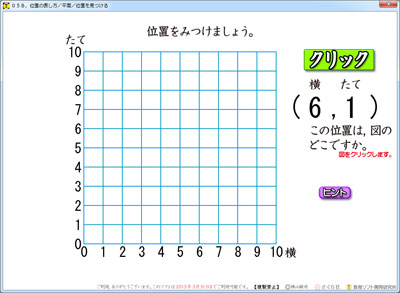
平面図形の位置を見つけるソフトです。
クリックをしてできた数を見て,それが座標のどこなのか,考えます。
「ここだな!」と分かったら,座標のその位置をクリックします。
正解だと,●がでてきます。
不正解だと,不正解音がなります。
こういうところは,できれば子ども達にクリックさせたい所です。
それには,ワイアレスマウス(無線マウス)があると便利です。
私自身も講演ではワイアレスマウスを使っています。それをフロアの先生方に手渡し,先生方にクリックしてもらっています。
緊張感,愉快感が断然良くなります。
ワイアレスマウスは,教室の必需品ですね。
--
ところで,平面座標の位置をなぜ「横,縦」の順に示すのでしょうか。長方形の面積のように「縦,横」としないのは,なぜでしょう。
こういう素朴なところは,なかなか教えてもらえにくいところです。
平面座標は,数直線が上下に拡張された概念なのです。
1年生の時に,10までの数や20までの数を習います。絵を伴った数直線も登場し,「数は並べて考えるんだ!」と教わります。この数直線は,100までの数で右に拡張されます。2年生で1000まで,1万までと学習し,右へ右へとどんどん拡張されていきます。
まるでアメリカの西部開拓のようでもあり,大航海時代のようにも思えてきます。
数が多くなると,表現上,横長になりすぎるので,中身の「圧縮」も行われています。
「拡張」と「圧縮」。
これは算数・数学の重要な考え方です。
「拡張」は,同様に大きくしても成り立つかな? と考える思考です。
「圧縮」は,大変だからチョー簡単に! と考える思考です。
「拡張」は冒険的な思考で,「圧縮」は面倒くさがり的思考です。
こういった人間くさいところがそのまま入り込んでいるのが算数なのです。
右へ右へと伸びた数直線。億や兆まで習うと,もう無限に右に伸びていくことが分かってしまいます。
それなら,「今度は左だ!」となるところですが,左は負の数になるので,中学までお預けです。これも,妙な話で,日常に負の数が頻繁に出る時代になっているですから,数直線を伴えば4年生ぐらいで負の数をガンガンと教えても問題ないはずなのです。
「負の数は中学から」
どうにも算数数学の都市伝説と思えてなりません。
左右への伸びが限界に来ると,突然変異的な拡張が始まります。
上下に伸びるのです。
左右とは全く質が違います。かなりぶっ飛んだ頭をしていないと,この手の拡張は生み出せません。
だから,意図的に教えていくことがとても大切となります。
上下の内,下は負の数になるので,教えるのは上にだけです。
これが,4年生で学ぶ平面座標です。
横に伸びてから上に伸びているので,これがそのまま「横,縦」という順の表記になったのです。
「突然変異的な拡張」の極めつけが,平面座標のすぐ後に登場してきます。
空間座標です。
空間座標ですから,実物を見せるのが一番良いのですが,伝達性を高めるには本などの平面上に表現します。三次元の物を二次元で表現するのですから,当然,無理が生じます。
その無理を乗り越えるのが「工夫」です。先達は縦の線を斜めに示す工夫をしました。この工夫は非常に画期的なことと,私は感動的に見ています。
空間座標のソフトも作り進める予定です。とても楽しいです。
この頃,良い本に良く出合っています。
この『扇 性と古代信仰』は面白いです。
小説のような書き方になっているので,「なんだか妙な本だな」と思いましたが,読み進めると,これが実に感動的です。
感動の一つは,吉野氏が退職をしてから研究して書いた本がこの本だと分かったことです。
退職をしたら静かな余生を・・・となりがちですが,「なぜ?」を追究する熱いハートがあると,専門書を書けるほどになるのです。
やっぱり,幾つになっても基本は同じです。
「熱いハート」と「フットワーク」と「読書」です。
もう一つの感動は,扇が性や神事と深い関わりがあるという吉野氏のひらめき,そのひらめきをどんどん証明していく痛快さがこの本にはあふれています。
現地での観察眼も素晴らしいですし,古典の読み方もとても勉強になりました。
こういったピンポイント専門書は,面白い物が多いですね。自分の興味の範囲では 「そろばん」と「箸」の本を読みましたが,両方とも得るところが多かったです。
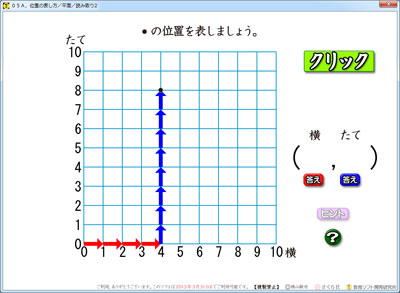
4年生で学ぶ,平面座標の位置を読み取るソフトです。
「●」の位置を(4,8)と,横・縦の順に数で答えます。
その仕組みに,子ども達が自分から気づいて欲しいと思い,「ヒント」ボタンを付けました。
「ヒント」ボタンをクリックすると,座標に矢印が登場します。
これだけでも,かなりわかりやすいです。
「分かる」とか「理解する」という頭の働きは,1回で成り立つ概念ではありません。最低,3回見る必要があります。
そこで,何度も見ることができるように,座標中の「●」と「矢印」が,マウスを追いかけるようにプログラムしました。
ですので,矢印が出ているまま,座標上でマウスを動かすと,矢印がどんどんかわります。これを見ているのも楽しいです。
その赤矢印と青矢印は,あるきまりに従って出てきます。
そのきまりに子ども達はすぐに気がつきます。
「まず,横に行って,それから上に行く」「上じゃなくて,縦だよ!」
「まあ,そうとも言うね」
答えも見ながら,矢印を見ることもできるので,とってもわかりやすくなります。
--
不思議に思うことは,座標の場合は「横,縦」の順になります。
それなら,長方形の面積の公式も「横×縦」と,まず,横から始まるようにすれば,あれこれ整合性が良くなると思うのですが,この2つは逆の流れになっています。
このあたりは面白いところで,材料を集めると,ちょっとした論文が書けますね。
『日本人に一番合った英語学習法』
この本も,竹村先生とのやりとりで購入を決めた本です。
読んでいるうちに,「根性あるな!」と感じた良い本です。
片言英語でなく,本格的な英語を習得するには,「素読」「暗唱」「多読」「文法」が基礎訓練と記されています。
ダメな方法はコミュニケーション重視の今の英語教育と示されています。
読んでいて,プログラム言語を習得したときの自分の学び方にかなり通じていたので,納得度は高かったです。
本格的に学ばない限り,絶対に習得できないのがプログラムです。日常会話ができればいいでしょう,と言う程度の片言プログラムでは,決められた範囲の作品しか作れません。ここはこうして,あそこはこう動かして・・と,目的に合わせた納得できる作り込みができないのです。
このあたりが,この本の論理とよく似ていて,驚きました。
私が学んだプログラム言語の場合は,とにかく「文法」と「単語」の習得がカギとなっていました。
「文法」も「単語」も,ちょっとでも間違えると,ソフトは意図したように動きません。たいていはエラーとなり,全く動かなくなります。
「文法」「単語」を覚え,それを実際に使って何度も何度もソフトづくりを体験することです。その数多くの体験が,この本の言う「多読」であり,「暗唱」なのだろうと,感じていました。
この本で,英語と日本語は非常に距離の遠い言語だと分かりましたが,プログラム言語も日本語とはかなり距離があります。
代数の数式のような「代入」が文法の中心になっているので,目の前に書いてある1行が,実は別の所に書いてある数十行の意味となっていることが,ざらにあります。
思考回路が言葉を使っているというより,謎解きをしているという感覚に近くなります。
どうにもならないほど頭を使うので,「脳の筋トレをしている」と言っていたこともありました。
そんな大変な状態に何度も陥ってしまうのですが,それでもプログラムを打ち続ける自分がいます。算数をもっともっと面白い勉強にしたいという思いが私にはあるからです。
この本は,そういう強い意志に関わることも記されています。
問題は,こういう強い意志を人はどうやって獲得するのか,ということです。
いろいろと興味の枠を広めてくれた,実によい本です。
英語の先生をしている友達がいます。
竹村和浩先生です。
メーリングリストで情報交換をしていたら,竹村先生の英語の指導法が,私の漢文の読み方に似ていることに気がつきました。それで英語の勉強関係の本を少し紹介してもらいました。
右の本は,その中の1冊です。
「列伝」ですので伝記です。新渡戸稲造,岡倉天心,鈴木大拙など,著名人の英語学習記が記されています。
読んでいる最中から,妙に力が湧いてきます。自分も,今やっていることをもっとしっかりやろう!という気持ちになってきた本です。
それで,張りきって,プログラムを書きまくっています。
エンジン全開の方向へ気持ちを高揚させたい方にお薦めの本です。
竹村先生とは, facebookでも交流をしています。
朝の東京の風景写真がアップされています。これが良い感じで,癒されています。
facebookは簡単につながることができて,なかなか面白いです。
facebookをされていましたら,お気軽に友達リクエストをお送り下さい。お待ちしています。
4年生の「直方体と立方体」のソフト開発が順調に進んでいます!
「辺の平行」を学ぶとき,もっとも重視されるのは,直観です。
パッと見て,平行と感じる辺が平行なのです。
ですので,平行がなんなのか,よく分かっていないと,かなり辛くなります。
そんな子でも,平行が感覚的に分かるようにと,作り込みました。
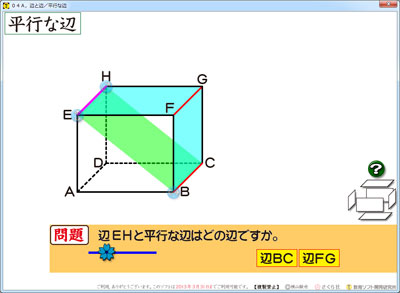
ご覧の通り,辺に色が付くようにしてあります。
そうして,立体での平行を感覚的にとらえられるようになったら,そこに論理をくっつけていきます。
「ところで,なんで平行といえるの?」などと,問うてみましょう。
「それはこの2つの辺は長方形の向かい合った辺になっているからです!」と答えてくれば,合格です!
でも,辺BCのように,反対側にある辺は,すんなりとは説明できません。
そこも直観的に理解できるように,面にも色が付くように作り込みました。
右端にあるバラバラの面が,面への着色ボタンです。[?]ボタンをクリックすると,ナナメの面が登場します。
水色をたどると,
辺EH∥辺FG 辺FG∥辺BC となります。
そこから,
辺EH∥辺BC と導かれます。
黄緑を見ると,ストレートに
辺EH∥辺BC となります。
時間がとれる教室では,ちょっと論理を楽しんでみるのも良い授業になりますね。
すると,黄緑の辺EBと辺HCも平行であることに気付く子も出てきますね。
さすが!の世界になります。
--
開発は順調に進んでいます。4年生の先生,ご期待下さい。
--




![キーワードでひく小学校通知表所見辞典[増補版] -2057文例◎ぱっと開いてすぐ書ける- CD-ROM付](http://www.kennya.jp/app-def/S-102/kennya/wp-content/uploads/2014/08/76-8.png)















