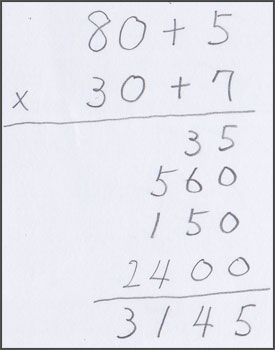チーム算数で，話しをし忘れたことがありました。
かけ算の筆算の話しです。

「８５×３７」を，右のように筆算したら，面白いでしょうね。

５×７
８０×７
５×３０
８０×３０
と，このように分解して計算するのですから，ちょっと面倒なやり方です。
でも，筆算の仕組みが実に良く示されています。

「２桁のかけ算はどうやるとできるのか」というような，問題解決の授業で，このような解答を出す子がいたら，グイッとうれしさが急上昇しますね。
多いにほめたくなります。

こういう筆算を説明するには，やっぱり図が必要です。
面積の図です。
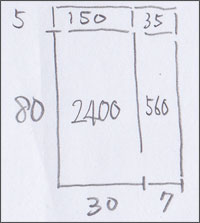面積図が理解できると，こういった計算の意味も分かり，（８X＋５）（３X＋７）の計算のやり方も，特に，難解には思わなくなるのではないかと思えています。

デカルトの『方法序説』に，複雑な物は細かく分けるという法則が載っていますが，こういうやり方も，その考え方に則していますね。
中学へつながる考え方なので，普通のやり方とは別に，こういうやり方もあることを示しておくのも有意義と思います。

こんなことを考えていたら，筆算の進化論みたいなことを感じてきました。
－－
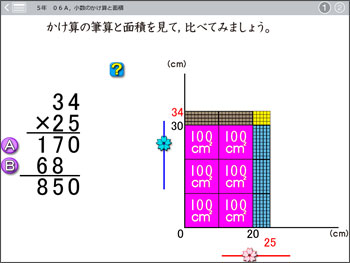似たような表現をしているソフトが５年生の算数ソフトにあります。
５年　小数のかけ算
「０６Ａ，小数のかけ算と面積」です。
こういう見方を何度か見て体験した子は，中学の因数分解の意味も伝わりやすくなりますよね。
クラウドを使っている先生，かけ算の筆算のおりに，学年を超えて，ちょっとこのソフトを見せてみるのは，いかがでしょう。
一瞬ですが，知的な算数が教室にやってきますね。