先日,佐々木先生とお昼を一緒に食べました。神保町の「さぼうる」という喫茶店です。
食事話の一つに,佐々木先生が円周率を考える場面でソフトを使ったことを話してくれました。
この話が,実にグッドでした。
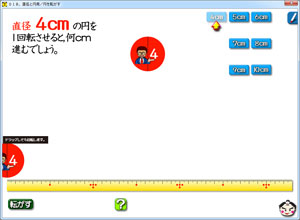
円を1回転させたら,何cm進むかを子どもたちに予想させたそうです。
そうしたら,3つ4つの円を転がしたあたりになると,子どもたちが,「先生,3倍とちょっとでしょ」と声が上がってきたそうです。
これは,すごいことです。規則性を見いだしているのです。「直径」と「1回転距離」との関係が,どうも「3倍とちょっとだ!」と把握できたのです。こういう発見が円を転がす様子を見せることで,つかめるのですから,実にすばらしいです。
円は,右上の水色ボタンで4cm~10cmまで自由に選べます。転がし方は,「自動的に転がす」「ドラッグして転がす」の2つから選べます。
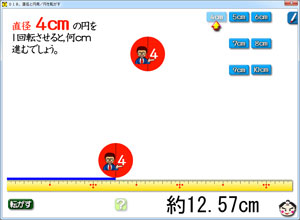
直径4cmの円を転がすと,12cmと半端。
直径5cmの円を転がすと,15cmと半端。
直径6cmの円を転がすと,18cmと半端。
直径7cmの円を転がすと,21cmと半端。
こうやって順に見ていけば,どうも3倍とちょっとかなと子どもたちが感じたのです。さすがです!
佐々木先生の話の重要なポイントは,「順に見せる」という方法です。順番に見せたから,気がつきやすかったのだと思います。大事な「指導法」です。
佐々木先生のおかげで,順に回転させていけば,どのクラスでも子どもたちの中から規則性・関係性を見いだす子が出てくるのです。うれしい方法を教えてもらいました。感謝です!
算数の思考で重要なことの一つが,「規則性の発見」です。「関係性の発見」といっても差し支えありません。AとBの間にどんな関係があるか,そういう思考が働く子を育てるのも,算数の授業の大切な点です。問題を見て,「『直径』と『回転距離』に関係がありそうだ!」と察する子が出てきたら,頭が算数モードになっています。ほめてあげるべき思考です。
算数ソフトのどのソフトでどういう規則性・関係性を子どもたちが見いだしたか,こんなところも,新しい算数の会で少しずつ出し合っていきたいと思っています。新しい指導法を模索できるのですから,とてもうれしいです。週末には,新しい会を発足したいと思っています。
------------
上のソフトは,『子どもが夢中で手を挙げる算数の授業』(さくら社)の5年1巻に収録されています。単元「円周」の中の「01B,直径と円周/円を転がす」です。

![キーワードでひく小学校通知表所見辞典[増補版] -2057文例◎ぱっと開いてすぐ書ける- CD-ROM付](http://www.kennya.jp/app-def/S-102/kennya/wp-content/uploads/2014/08/76-8.png)















