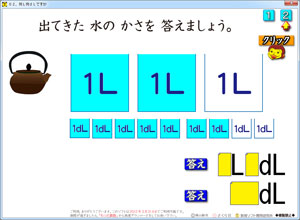
２年生の「水のかさ」の２本目のソフトです。
右上のボタン１，２は，次の様になっています。
－－－－－－－－－－－－－－－
１：何Ｌか答える（最大６Ｌまで）
２：何Ｌ何ｄＬか答える（最大３Ｌ９ｄＬまで）
－－－－－－－－－－－－－－－
クリックをすると，水が土瓶（鉄瓶かも）から飛び出してきます。
水は，飛んでくるときから小分けされているので，すごい子は水が着地する瞬間に答えられるかもしれません。先生のちょっとしたアイデアで，子ども達も盛り上がって答える場面が作れます。ぜひ，楽しくご活用ください。
「２」ボタンの方では，ごらんのように，答え欄が２つあります。
２Ｌ７ｄＬと，２７ｄＬ。
両方が上下に示されるので，単位の換算の素地が身につきます。
これから指導に入る先生，どうぞ，ご活用ください。
もう，単元が終わっている先生，朝自習の時間にでも，復習として子ども達に見せるのもよい学習になります。
「もっと！算数」サイトにアップしました。ぜひ，ご覧ください。
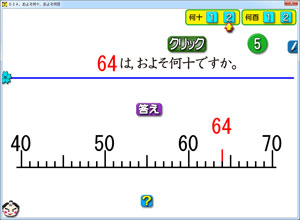４年生の概数。
要するに，「どっちに近いか？」ということを，「四捨五入」の概念で判断できるようにする，そういう学習です。
この勉強は，パッと見，とても簡単そうに感じます。ちょっと教えれば，直ぐにわかるような気がします。
でも，現実はなかなか厳しく，わからない子はわからないのです。
このソフトを開発する前から，「どっちに近いか？」を感覚的にとらえられるソフトを作りたいと思っていました。ただ，その表現をどうするかが難しく，どう表現したら子供達にわかりやすいかで，結構頭を使いました。
そうして，作り上げたのが，このソフトです。
「答え」ボタンをクリックすると，何かが動き出します。さて，何がどう動くのでしょうか。
このソフトを持っている先生は，上のような問いを子供達に出すことができます。
上の形より，もっと粗っぽく「「答え」ボタンをクリックすると，どうなるでしょう」でもかまいません。
どちらにしろ，子供達は学習ゾーンで答えてくれます。「当て推量」の答えになるのですが，その当て推量も「ソフトは何かを教えようとしている」という理解があるので，学習から外れた方向に向かうことはありません。
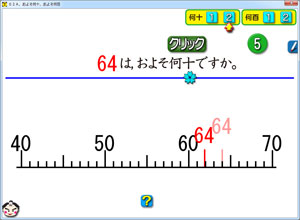そうして，実際に「答え」ボタンをクリックすると，赤文字の「６４」が動き出します。「６０」に吸収されるように動きます。
これを，何回か見ている（最低３回です）と，「近い方に動く」というきまりが見えてきます。
このきまりが見えてきたら，第一段階突破です。
算数は，「きまり」で成り立っている勉強なのですが，そのきまりは「数」や「計算」などにまつわるきまりです。
ですから，「近い方に動く」という日常語でのきまりが出てきたら，「数を使ってきまりを考える」方向に導きます。すると，「四捨五入」の概念に近づく事ができます。
算数ソフトが手元にある先生は，こうした「きまり」に直行する指導ができます。
※ 上の算数ソフトは，『子どもが夢中で手を挙げる算数の授業』（４年５巻）に収録されています。
「算数」は，どういう教科でしょう。
こういう根本的なところがバシッと把握できていると，授業の腹の据え方がしっかりしてきます。
一言で言うと，算数は「きまり」で成り立っている教科です。
「きまり」と言っても，主に「数」「計算」という非常に抽象的な世界でのきまりです。
この「きまり」を理解し，使えるようにし，さらに高いレベルの「きまり」へと頭で理解できるように進んでいくのが，算数なのです。
また，算数の単元は大筋４つの段階を経て進んでいきます。
１） 理解
２） 定着
３） 応用
４） 実用
まず，算数の「きまり」を理解します。
次に，その理解したことが定着するように学習します。
それから，きまりを利用して，ちょっと複雑な問題をも解けるようにします。
そうして，できれば，生活でも使えるようにしていきます。
「きまり」の勉強を「理解」するとき，もっとも重要になることは，何でしょう。
その答えは，「きまり」を見いだすことです。
もう少し，強く言えば，「きまり」を見いだせる能力を育てることです。
筑波大付属小で教鞭を執られていた坪田耕三先生も，正木孝昌先生も，「きまり」に注目をしています。きまりを見つける能力をどうやって伸ばしていくのかについて，素晴らしい実践をされてきています。
「数的きまり」や「計算的きまり」，また，「数値化できる規則性」を見いだせるように指導をすることが，子供達の算数の理解力を高めることになります。
そのときに顔を出すのが，「最低３回の論理」と「関係性の視覚化」です。まさに，デカルトの論理です。
私の作っている算数ソフトは，繰り返しが容易なため，この「最低３回」の論理に強いのです。また，具体と数，数と式，数とグラフなど，関連性を持った相異なる２つを同時に見せているの，両者の関係がつかみやすいのです。これにより，きまりの理解が容易になっているのです。
少し歴史的に言うと，デカルトが４００年前に見いだした論理を，算数の世界で誰にでも適用できるようにしたのが，算数ソフトなのです。
デカルトの『精神道の規則』です。
この本には，反復練習の最低回数が３回であることが論理的に示されています。
そこを読んだときには，うなりました。関係性として把握すれば，確かにその通りと，ストンと腑に落ちたのです。
それまでは，「桃太郎の繰り返し」の論理で感覚的に３回必要と把握していました。でも，なぜ３回なのか，そこをつっこまれると答えに窮する状態でした。
それが，論理的に説明できるようになったのです。私にとっては，画期的なアウフヘーベンでした。
まさに，「すごい」の一言です。
『精神指導の規則』は，私にとって，「理解指導の方法」として迫ってくる本なのです。
子ども達が算数の何かを理解するということは，どういう事なのか，それが記されているとっても重要な本なので，時々講演などでも紹介しています。
先だって兵庫で開催された教材授業開発セミナー全国大会での講演でも紹介しました。ただし，難しくてなかなか読めないから無理することはないと付け加えました。
でも，なかなか読めなかったのは私だけかもしれないので，ここに紹介することにします。講座で関心を持った先生，この本があのとき紹介した本です。
私の好きなところを，ちょっと引用してみます。
「規則第九
精神のすべての力を極めて些細な容易な事物に向けるべきである，そして，我等が真理を判明に明瞭に直観するに慣れるまで，長くそこにとゞまるべきである。」
この後に，詳しい論述が展開されています。すごいですよ。
算数ソフトを使うと，理解が容易に進むことが，こういった章をよむことで，確かに！と伝わってきます。
算数ソフトは単に時代の生んだ新しい教材と言うだけでなく，理解の指導に非常に優れた教材であることが，よくわかります。
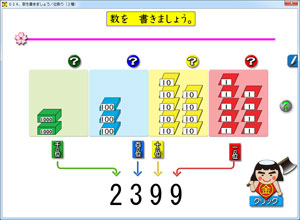今年の夏休みは，「算数ソフトの話」をあちこちでしています。
どこの会場でも，算数ソフトは大人気です。やっぱり，面白いというのは，最高です。
埼玉の毛呂山町の研修では，右の画面をお見せしました。
赤い色の「？」ボタンをクリックすると，折り紙が１枚増えます。すると，どうなるでしょう？？？
こういう所は，授業として「おいしいところ」です。このおいしさを，ソフトを使っているクラスでは簡単に子ども達にも分け与えることが出来ます。しかも，何回でも！！
おいしいところが見つかったら，授業の日が待ち遠しくなります。先生のうれしさは，子ども達にも伝わり，授業はとっても良い感じですすみます。
しかも，単においしいだけでなく，クリックしながら，数の仕組みがわかるのです。
嬉しい限りです。
数は実に淡泊ですが，量が伴い，変化が伴うと，急に意味深いものに変わってきます。
大いに算数ソフトを使ってほしいと願います。
－－
算数ソフトの講演先で，徹底反復学習で有名な広島の山根僚介先生と一緒になりました。３０代の若さですが，落ち着いていて，実践の積み重ねもしっかりしていて，これから先が楽しみな先生と思いました。
山根先生とご挨拶をしたとき，『尋常小学校を体験！ 残しておきたいこの授業』（ＰＨＰ）を持っていました。この本は，とても思い出深い本です。サインをしてお話を伺ったら，山根先生は算数数学が得意で，歴史も大好きなのだそうです。
今度お会いしたときには，もう少しじっくりお話をしたいと思います。
九州の書店で，店員さんとお話ししたときに，「面白いですよ」と一言お言葉をいただいたので，買ってみました。
和算関連の本であることは，絵柄を見れば直ぐにわかります。また，江戸時代に「算法少女」という和算書があったことは知っていましたので，読んでみました。
この本は，江戸時代に書かれた「算法少女」という算術書を中心に描いた小説です。
調べ物の本と違って，まるで江戸時代そのものに案内されたような気持ちになってきます。
よく調べてあるなと，感心したのはかけ算九九の言い回しです。
「二五の十，二六の十二，二七の十四・・・」
九九を唱える時に，「が」と唱えるこのとの他に，「の」ととなえるときもありました。こういうところは，本当に詳しい人しか知らないところなので，遠藤寛子氏はさすがだなと感じ入りました。
鋭い指摘は，後半に出てきます。
関流・最上流などと流派の揚げ足取り的論争に突き進んでしまった和算家が，もっと広い視野で算術をとらえていれば・・・・。
同業者同士は，どうしてもライバルの心が出てきます。知らず知らず，流派のようなものができて，そこを軸に考えを進めるようになります。そこを超えて進む人が，次の時代を拓いて進むのだと思います。
