このソフトは，「コラボソフト」です。授業をされる先生と，ソフトを開発する私とで協力して作っているコラボレーションソフトです。
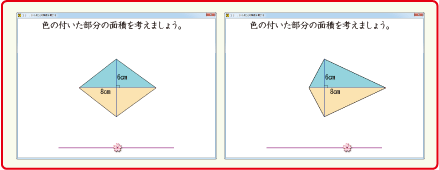
５年生でひし形の面積を学びます。ひし形まで学習すると，後は応用となります。このソフトは，その応用場面に良い感じのソフトです。
対角線の横が，その長さを一定にしたまま，左右に動きます。
すると，「ひし形」が「たこ形」になります。
もっと端まで動かすと，へこんだ形の「へこみ形」になります。
それでも，面積は同じです。
どうしてだろうかと考えれば，面積を求める式に使う所の長さが変わっていない事に気付きます。
そこから，もしかしたら・・・などと，自分なりの仮説が生まれます。この場合の仮説は，もちろん算数的規則性の仮説です。
授業は面白くなっていきます。
こういう思考系の問題も，ソフトで上手く作ると授業は変わってきます。連続して変化する様子を見ることができると，思考できる範疇が極めて大きくなるからです。
これは，思考範囲の拡大化をもたらします。研究領域がここにも大きく広がっていることが分かります。
やる気のある先生方とコラボしながら，算数ソフトを開発する時代に次第に向かいつつあります。
私も微力ですが，算数ソフト愛好の先生方と，実践的にコラボソフトを開発していきたいと思っています。
面白い時代になりましたね！！
１０年ほど前に，話題となった本『分数ができない大学生』です。
１０年前にも，指導要領が改訂になり，学力低下がひたひたと歩み寄っていた頃です。
生活科などもまだ元気だった頃です。
もっと算数・数学の力を！と打ち出したこの本は，タイトルが実に衝撃的で，日本国中に「こりゃ，いかん！」という思いが走りました。
その本が，１０年目にして新版になったので読んでみました。
算数・数学ができない学生が増えていることの報告が著者の先生方から次々に示されています。
その現状を何とかするために，数学の必要性や重要性，知っていると得をするということも示されています。
こういう大きな文脈の話しも面白いのですが，この本は随所に「ああ，いいね！」と思えることが書かれています。
そんなかで，私が感じ入ったのは，次のような言葉です。
◆ 数学は，一つ事を学ぶと，それ以前に学んだ初等的な内容の理解を確実にする。
当たり前と言えば，あまりにも当たり前のことです。
でも，これがなかなか見えないのです。
先日，５年生の立体のソフトが話題になりました。
立体をドラッグして動かすと，立体の重なりの様子が見えます。
それを見て，子ども達の中には，１ｃｍ３の立体が何個あるか数える子が出てきます。
何段にもなっているので，それはかけ算で・・となります。
こういう学習をしているときに，「立体の体積について理解できたか」という事の他に，「立体以前に学んだ何かを確実にしている」という視点を持つと，実に豊かな学習をしていると分かります。
算数って，素晴らしいと感じてきます。
山口のセミナーへ行ったときのことです。主催者の藤本先生から，「算数ソフトを使った授業のやり方など発表する会を開きましょう！」と熱い御提案を頂きました。
その声を聞いてか，セミナーで算数ソフト活用の実践発表をした佐藤先生が「こんな事があった！」「あんな事があった！」と熱く語っていました。
わき出るように，いろいろなビックリする出来事が続きました。
これほど，良いことがたくさん起こるのですから，やっぱり，そういうセミナーを開こう！ということで，山口の夜は多いに盛り上がりました。
そうして，今，計画を進めているのが「奇蹟の算数セミナー」（仮称）です。 １１月開催予定！
「チーム算数」で城ヶ崎先生，佐々木先生に，内容の相談をしたら，どんどん良い意見が出て，これまでにない，とっても充実するセミナーになりそうです。（詳しいことは，確定し次第，お知らせします）
お話しをしてくださる先生方は，算数ソフトを長年使っている腕利きの先生方です。
一つ一つのお話しに，納得感のある指導技術や指導感，授業への哲学思想が学べると思います。
「奇蹟の算数セミナー」開催に向けて，「算数数学好きにする会」のメーリングリストで情報交換を進めています。新たに，佐藤先生，渥美先生，上澤先生にご入会いただき，ＭＬもパワフルになっています。
－－
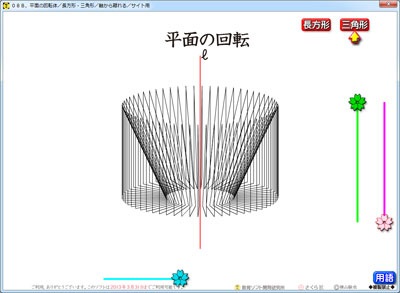
中１の数学「空間図形」のソフトを，近々，「もっと！算数」サイトにアップする予定です。
このソフトを見れば，回転体の意味が伝わります。図形の連続が巻き起こす面白さがしっかり伝わります。
この回転体のソフトもインパクトが強いので，数学嫌いな生徒たちも視線が釘付けになります。
そういうときは，その気になっているときです。あれこれ先生が解説したり，生徒に考えを言わせたり，ノートに書いたり・・・。良い感じで授業進みますね。
復習で見せるのも，非常に効果的です。
中学校の先生，アップされたら，ぜひご覧下さい。そうして，生徒さんにぜひ見せて上げてください。
毎年，どこかで発表をされている和歌山の奥田吉彦先生。
教材づくりのアイデアはピカ一です。
その奥田先生が，一目で分かる教材として算数ソフトが群を抜いていると，高く評価して下さっています。
この評価で十分に嬉しいのですが，さらに，「教材はこうあるべきである」と，まるで模範的教材であるかのように話されています。
大感激です。
とても嬉しい気分になって，ソフト開発を進めました。
気分が良いと，作りも快調です！
今回は，中学１年の数学のソフトです。
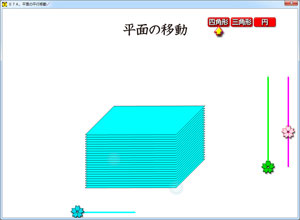
平面図形を垂直に移動させると，そこに立体ができることを見せるソフトです。
平面図形の形を変えられるので，グイッと絞れば，直線になります。もっと絞ると点になります。
その点や直線も移動できるので，
◆ 点が移動して直線になる
◆ 直線が移動して平面になる
というところも，見せることができます。
奥田先生はいつも元気を与えてくれます。
良い感じでソフトを作れました。ありがとうございます。
５年の体積ソフトをＣＤに収録しました。
合計９本のソフトが入っています。
－－－－
０１ ，直方体，立方体の体積／理解
０２ ，直方体，立方体の体積／公式を考える
０３ ，直方体，立方体の体積を求める／公式を使う
０４ ，Ｌ字型の体積を求める／工夫して求める
０５ ，１ｍ３は，１ｃｍ３何個分？
０６ ，高さ・横の長さと，体積の関係／比例
０７ ，１Ｌと容積
０８ ，方眼用紙と容積
０９ ，展開図と体積
－－－
この体積のＣＤ，山口の講座に持っていきます。
講座特別価格でおわけする予定です。
持っていくのは，たぶん１０枚ほどです。
これで，ダウンロードはどうも・・・と思われている先生方にも，教室で楽しく使っていただけます。
ＣＤなので，使い方はとても簡単です。
教室のＰＣにＣＤを入れれば，自動で起動します。目次画面が出てきたら，使いたいソフト名をクリックします。すると，ソフトが動き出します。
※ 「もっと！算数」にアップされている体積は，近々，終了となります。
仕事が一段落したので，教育論の本を読み始めたのだが，これがあまり面白くありません。
顔を上げたら，そこに『五経・論語』があったので，それを取り出し，ぱらぱら読みました。
礼記のところで，孔子が仇討ちについて弟子に話しています。親の敵がいるような所へは仕官しないのです。 孔子がこういうのですから，普通の人は敵がいても仕官できるのなら，敵に気付かなかったことにして，まずは飯の心配を無くすことを選んでいたように思えます。面目より飯と考えるのは自然な成り行きです。
そう思うと，孔子は日本の武士道に近い感覚を持っていたようにも思えます。
さらに，パラパラとめくったら，『春秋左氏伝』の初っぱなのページが偶然開きました。
『春秋左氏伝』というのは，今から３０００年ほども前のことを記した中国の古典です。その初っぱなから，分数の概念が出てきます。
国の中に邑があるのですが，大きい邑でも，国の三分の一を超えず，中の邑なら五分の一，小は九分の一と昔から決まっていると述べられています。
読んでいる本は日本語訳ですので， 本当に分数が使われていたのかどうか，ちょっと疑問が走ったので，インターネットで調べてみました。中国のサイトです。
運良く，左氏伝を紹介しているサイトと出合いました。
「大都不過參國之一，中五之一，小九之一。」と載っていました。
ただの三分の一ではありませんでした。「三国の一」でした。中国語に詳しくありませんが，分母に単位「国」が付いていると受け止められます。面白い表現です。
一度単位が付いたら，即座に続く所では，「五の一」「九の一」と単位を省いています。これも勉強になります。
省略しても意味が通じるなら，それで良いと考えているのだろうと思えてきます。読み手の補う力を活かした記述とも思えます。
ここに来て，急に日本の古い本が気になりました。
『豊後国風土記』を開きました。７００年頃の記録ですので，今から１３００年ほど前の作品です。
分数と思える記述は「分両国」とあるぐらいで，国が二つに分かれるという話しです。分数以前の段階です。
左氏伝の「五之一」は，昔からこの広さを超えないのがしきたりで，これを超えると，国が危なくなるとされています。ということは，３０００年よりずっとずっと昔から，中国では分数が問題なく使われていたことになります。
昔の中国は算数数学大国だったことが，こんな所からも伝わってきます。
教育論の本は面白くないのですが，また，続きを読みます。つまんないと感じる本を読むことも，面白い本への興味を強める妙な効果があるからです。
