４年生の空間座標。
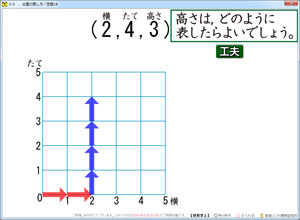
ちょっとわかりにくさが生じるのが，「縦」です。
平面座標の時には，真っ直ぐ上に伸びていた縦なのですが，それが空間座標ではナナメに伸びていきます。「高さ」にその場所を譲るためです。
そこがうまく理解できない子もいるので，平面座標から空間座標へと変わる様子をアニメーションで見えるようにしました。
[工夫]ボタンがあります。
これをクリックすると，正方形の座標が右に４５度傾きはじめます。その時には青の矢印も 一緒に傾きます。
青の矢印は縦を示しているので，縦がナナメになったとつながります。
こうして，縦は平面では真上だが，空間になるとナナメで表現することを理解していきます。
では，新しく登場した「高さ」はどうなるのでしょう。
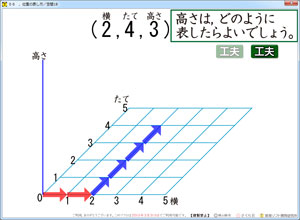
２つめの[工夫]ボタンをクリックすると，上に伸びるアニメーションが始まります。
この時，床のような平面が１枚登場します。
その平面が１メモリ上に上がると，また１枚登場します。
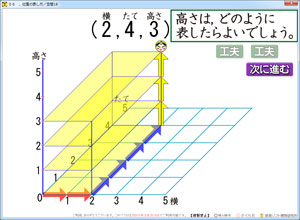
そうして，最後に桃太郎がでてきます。桃太郎の位置が（２，４，３）の示す位置となります。
この様子を見ると，ビルやマンションや立体駐車場の１階，２階と類似した感触を子どもは持ちます。
建物での階層の数え方は，算数とはちょっと違う数え方になっています。スタートが「１」なのです。地上と同じ階が「１階」となります。
建物の階数の呼び方は，生活から生まれたので自然数の考え方が当てはめられています。
自然数というのは，皆さんもご存じのように，１，２，３，４・・・と，１から始まります。
これに対して，座標は数学上で生まれてきた概念なので，基準となる点は「０」となっています。原点ですね。０が基準になっているので，座標では正の数も負の数も小数も・・何でもスッキリと表現でき，大変便利な思考ツールになっています。
このソフト，工夫を見た後，[次に進む]ボタンが登場します。
それをクリックすると，空間座標の読み方が学習できるようになっています。
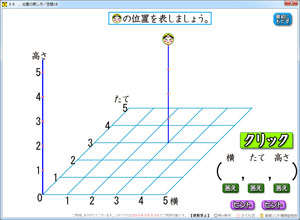桃太郎の位置を「横・縦・高さ」の順に数で表現する学習です。
空間の表現を理解を一層深めてもらえるように，ヒントを用意しました。
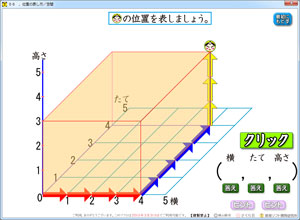ヒントは２種類！
【ヒント１つめ】
矢印が出ます！
このヒントで読み進め方がしっかり分かります。
【ヒント２つめ】
直方体が出ます！
同じ単元で学んだ直方体の見取り図が，空間座標の読み方に役立ちます。
ヒントを両方見せると，なるほど感がグッと高まりますね。
－－
算数ソフトを使う先生がどんどん増えています。
算数が大好きになる子もどんどん増えています。
とても，嬉しいです！
◆ ＤＶＤ算数ソフト『子供が夢中で手を挙げる算数の授業』
◆ 「もっと！算数」サイト
もっともっとたくさんのクラスで使って欲しいと願っています。
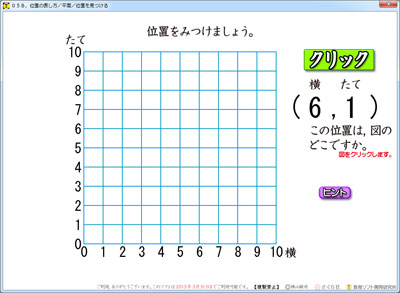平面図形の位置を見つけるソフトです。
クリックをしてできた数を見て，それが座標のどこなのか，考えます。
「ここだな！」と分かったら，座標のその位置をクリックします。
正解だと，●がでてきます。
不正解だと，不正解音がなります。
こういうところは，できれば子ども達にクリックさせたい所です。
それには，ワイアレスマウス（無線マウス）があると便利です。
私自身も講演ではワイアレスマウスを使っています。それをフロアの先生方に手渡し，先生方にクリックしてもらっています。
緊張感，愉快感が断然良くなります。
ワイアレスマウスは，教室の必需品ですね。
－－
ところで，平面座標の位置をなぜ「横，縦」の順に示すのでしょうか。長方形の面積のように「縦，横」としないのは，なぜでしょう。
こういう素朴なところは，なかなか教えてもらえにくいところです。
平面座標は，数直線が上下に拡張された概念なのです。
１年生の時に，１０までの数や２０までの数を習います。絵を伴った数直線も登場し，「数は並べて考えるんだ！」と教わります。この数直線は，１００までの数で右に拡張されます。２年生で１０００まで，１万までと学習し，右へ右へとどんどん拡張されていきます。
まるでアメリカの西部開拓のようでもあり，大航海時代のようにも思えてきます。
数が多くなると，表現上，横長になりすぎるので，中身の「圧縮」も行われています。
「拡張」と「圧縮」。
これは算数・数学の重要な考え方です。
「拡張」は，同様に大きくしても成り立つかな？ と考える思考です。
「圧縮」は，大変だからチョー簡単に！ と考える思考です。
「拡張」は冒険的な思考で，「圧縮」は面倒くさがり的思考です。
こういった人間くさいところがそのまま入り込んでいるのが算数なのです。
右へ右へと伸びた数直線。億や兆まで習うと，もう無限に右に伸びていくことが分かってしまいます。
それなら，「今度は左だ！」となるところですが，左は負の数になるので，中学までお預けです。これも，妙な話で，日常に負の数が頻繁に出る時代になっているですから，数直線を伴えば４年生ぐらいで負の数をガンガンと教えても問題ないはずなのです。
「負の数は中学から」
どうにも算数数学の都市伝説と思えてなりません。
左右への伸びが限界に来ると，突然変異的な拡張が始まります。
上下に伸びるのです。
左右とは全く質が違います。かなりぶっ飛んだ頭をしていないと，この手の拡張は生み出せません。
だから，意図的に教えていくことがとても大切となります。
上下の内，下は負の数になるので，教えるのは上にだけです。
これが，４年生で学ぶ平面座標です。
横に伸びてから上に伸びているので，これがそのまま「横，縦」という順の表記になったのです。
「突然変異的な拡張」の極めつけが，平面座標のすぐ後に登場してきます。
空間座標です。
空間座標ですから，実物を見せるのが一番良いのですが，伝達性を高めるには本などの平面上に表現します。三次元の物を二次元で表現するのですから，当然，無理が生じます。
その無理を乗り越えるのが「工夫」です。先達は縦の線を斜めに示す工夫をしました。この工夫は非常に画期的なことと，私は感動的に見ています。
空間座標のソフトも作り進める予定です。とても楽しいです。
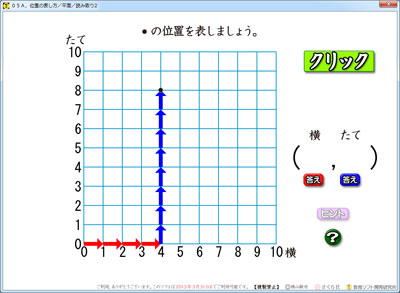
４年生で学ぶ，平面座標の位置を読み取るソフトです。
「●」の位置を（４，８）と，横・縦の順に数で答えます。
その仕組みに，子ども達が自分から気づいて欲しいと思い，「ヒント」ボタンを付けました。
「ヒント」ボタンをクリックすると，座標に矢印が登場します。
これだけでも，かなりわかりやすいです。
「分かる」とか「理解する」という頭の働きは，１回で成り立つ概念ではありません。最低，３回見る必要があります。
そこで，何度も見ることができるように，座標中の「●」と「矢印」が，マウスを追いかけるようにプログラムしました。
ですので，矢印が出ているまま，座標上でマウスを動かすと，矢印がどんどんかわります。これを見ているのも楽しいです。
その赤矢印と青矢印は，あるきまりに従って出てきます。
そのきまりに子ども達はすぐに気がつきます。
「まず，横に行って，それから上に行く」「上じゃなくて，縦だよ！」
「まあ，そうとも言うね」
答えも見ながら，矢印を見ることもできるので，とってもわかりやすくなります。
－－
不思議に思うことは，座標の場合は「横，縦」の順になります。
それなら，長方形の面積の公式も「横×縦」と，まず，横から始まるようにすれば，あれこれ整合性が良くなると思うのですが，この２つは逆の流れになっています。
このあたりは面白いところで，材料を集めると，ちょっとした論文が書けますね。
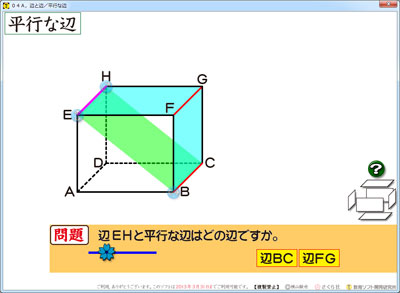
４年生の「直方体と立方体」のソフト開発が順調に進んでいます！
「辺の平行」を学ぶとき，もっとも重視されるのは，直観です。
パッと見て，平行と感じる辺が平行なのです。
ですので，平行がなんなのか，よく分かっていないと，かなり辛くなります。
そんな子でも，平行が感覚的に分かるようにと，作り込みました。
ご覧の通り，辺に色が付くようにしてあります。
そうして，立体での平行を感覚的にとらえられるようになったら，そこに論理をくっつけていきます。
「ところで，なんで平行といえるの？」などと，問うてみましょう。
「それはこの２つの辺は長方形の向かい合った辺になっているからです！」と答えてくれば，合格です！
でも，辺ＢＣのように，反対側にある辺は，すんなりとは説明できません。
そこも直観的に理解できるように，面にも色が付くように作り込みました。
右端にあるバラバラの面が，面への着色ボタンです。[？]ボタンをクリックすると，ナナメの面が登場します。
水色をたどると，
辺ＥＨ∥辺ＦＧ 辺ＦＧ∥辺ＢＣ となります。
そこから，
辺ＥＨ∥辺ＢＣ と導かれます。
黄緑を見ると，ストレートに
辺ＥＨ∥辺ＢＣ となります。
時間がとれる教室では，ちょっと論理を楽しんでみるのも良い授業になりますね。
すると，黄緑の辺ＥＢと辺ＨＣも平行であることに気付く子も出てきますね。
さすが！の世界になります。
－－
開発は順調に進んでいます。４年生の先生，ご期待下さい。
－－
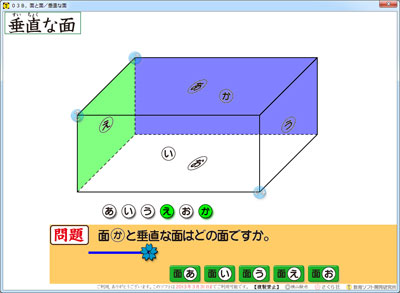
「直方体と立方体」の単元で，面と面の関係も学びます。
「垂直の関係」と「平行の関係」です。
良い感じで作り進んでいるのが，垂直の関係にある面を学ぶソフトです。
問題コーナーの[桜]スライダーで，基準となる面を決めます。
「あ～か」まで，サクサクと選ぶことができます。
今は「か」と垂直な面を出題しています。
その出題された「面か」がどれだかわかりにくい子がいたら，立体のすぐ下にあるボタン「か」をクリックします。すると，ご覧のように「面か」が紫色になります。
この面に垂直な面を考えるのが学習です。垂直ですから，９０度の関係です。
もしかしたら「面え」かな？ と思ったら，ボタン「え」をクリックして確かめることができます。
そうして，自信が付いたら，色を付けないで問題コーナーの面のボタンをクリックしていきます。
ここでも，直方体の大きさを変えられるように，頂点に３カ所ボタンが付いています。
立体が細長くなっても，立方体になっても，垂直の関係には関係がないことが分かれば，それは一つの学びとなります。
－－
ソフトで学習をすると，「中身が楽しい」「短時間でできる」などの特徴があるので，「面あ」を学習したら，続いて「面い」もやりたくなります。すると，つられて「面う」も「面え」もやりたくなり，ついには，「面お」「面か」には「先生，まだやってません！」と「出題おねだり」が始まります。
こういうグッと来る良い雰囲気。たまらない一時ですよね。
そうして，６面分を順次やっている内に，ある決まりに気付きます。
・１つの面について，４つの垂直の面がある！
「きまりを見つけるのが算数！ さすがです！！」と，うんとほめることができますね。
－－
このソフトの開発も，順調に進んでいます。４年生の先生，ご期待下さい。
４年生の単元に，「直方体と立方体」があります。
この単元で「面の平行」を学習します。
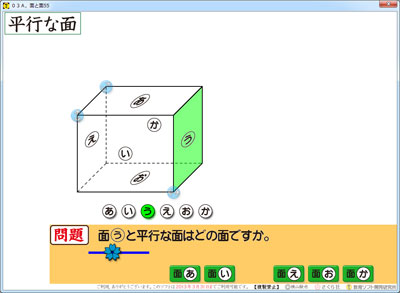
たとえば，「う」の面と平行な面はどれなのかを考えさせる学習です。
でも，この学習場面。ちょっと辛いところがあります。
面の番号を言われても，どれなのか・・・となる子がいることです。
そこで，ちょっとプログラムを書き加えて，面に色を付けるボタンを取り付けました。
立体の下にある「あ～か」のボタンが色つけボタンです。
「色つけボタン」をクリックすると，その面に色が付きます。
どの面が，今問題になっているのか。それがスッと分かりますね。
慣れた来たら，色を付けるボタンを使わずに，問題欄にある「面あ～面か」までのボタンで答えるようにします。
正しく答えられれば，「丸」がつくので，なかなか良い感じ勉強ができます。です。
問題を出すとき，「あ～か」のどれかを選べるようになっています。[桜]スライダーを左右に動かすだけで，問題を切り替えることができます。
これも，なかなかグッドになっています。
－－
「逃げるが勝ち」と言う諺がありますが，算数の場合は，「見せるが勝ち」です。
４年を担当されている先生，ソフトが完成したら，是非，使ってみてください。
