３年生であまりのあるわり算を学習します。
その学習の一つに，わる数とあまりの関係があります。
わる数 ＞ あまり
こういう関係があることを，子ども達にもしっかり理解してもらいます。
このような２つの数の関係は，たし算・ひき算・かけ算では，取り立てて教えることはありません。たし算で「たす数＜答え」という学習は特別にはしないということです。
あまりのあるわり算で，２つの数の関係（わる数＞あまり）を教えるのは，答えのミスを減らすためです。
１６÷３＝５あまり１ です。
これを，ちょっとした手違いで，１６÷３＝４あまり４ としてしまうこともあります。
教わった確かめ算をすると，３×４＋４＝１６となり，確かめもあっています。
しかし，「４あまり４」では，×です。
あまりの４が，まだ３で割れるからです。
わり算をするということは，「もう，これ以上割れないよね」という所まで行うのがルールになっています。
このルール，あまりの無いわり算（割り切れるわり算）の時には，ほとんど自覚されません。
かけ算九九の裏返しで，エイッと答えが出るからです。
わり算はかけ算をちょっと応用した程度の計算と思い，まずは一安心します。
しかし，続けて，次なるわり算，あまりのあるわり算が登場します。
ここで，新たなルール，「もうこれ以上割れないね，という所まで割る」がでてきます。
他の計算には無い新型ルールです。
これになじむのは，なかなか大変です。
この「これ以上割れないところまで割る」というルールをしっかり自覚してもらうために，わる数とあまりの関係を知ってもらうのです。
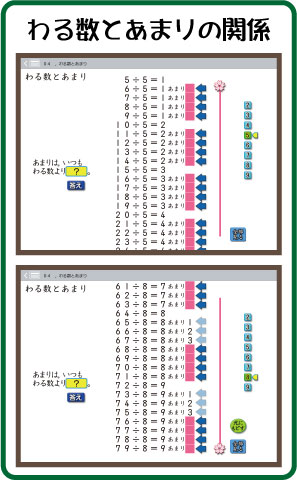「あまりは，わる数より小さいんだよ」
「わる数より，あまりが大きくなったら，まだ割れるって事だよ」
こう説明して，すっと分かる子もいます。
でも，分かって欲しい子は，なかなか分かってくれません。
言葉として伝わるのですが，「そうなんだ」という腑に落ちる所までなかなかたどり着かないのです。
わる数とあまりの一覧を見る経験が不足しているのです。
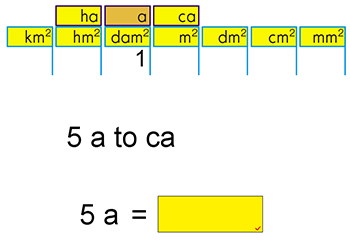
ソフト画像のように，わり算の式を並べると，あまりは１から順に数が大きくなっていると，すぐにわかります。
でも，途中まで大きくなると，突然，あまりは無くなり，また，１から順に大きくなります。
この様子を見ていくと，「÷５」のときは「４まで」，「÷８」のときは「７まで」，とその規則性に気がついてきます。
「÷３」のときは？
「÷９」のときは？
こうやって，複数のわる数の場合を見ていくことで，ようようにして，わる数とあまりの関係が把握できてきます。
「急がば，回れ」です。
言葉であっさりすまそうとするのは，急いでいる学習です。
中身がしっかりと伝わらないので，「そうなんだ」と腑に落ちない子が出てきます。
いろいろな場合を具体的に示していくことが，着実な歩みになります。
－－
今回のソフトは，算数クラウドの「３年→わり算（２）あまりのあるわり算→０４，わる数とあまり」です。
２の段～９の段までそろっているので，途中まで見ていく内に，みんな分かるようになったと，嬉しいお知らせを受けたことがあります。
クラウドをお使いの先生，ぜひ，子ども達に見せてあげてくださいね。
－－
★３年生のわり算，算数ソフトで教室中が大盛況！
関連記事：
聖徳太子や源頼朝など，昔の偉い人の絵を見ると，皆さん，手に細長い板を持っています。
これ，「笏（しゃく）」と言います。
有田和正先生のファンの先生方なら，この笏を見て，「あっ，カンニングペーパーね！」と思われたことでしょう。
平安貴族の仕事は儀式です。
式場には偉い方もいます。
そんな場で，自分が何か話すこともありました。
緊張のあまり話す言葉を忘れてはいけないので，その内容を笏の内側に書き，それを見ながら話しました。
でも，それだけではなく，記録するためにも使われていました。
偉い方から，「こんなことをよろしくね！」と言われたら，それを忘れないように，笏の内側にメモしていました。
そういうことが，『江家（ごうけ）次第』（江という家の年中行事の式次第が記されている書）に書いてあると，かの有名な『貞丈（ていじょう）雑記』に記されています。
－－
君の仰せを忘れぬ為に書き付けて吾が奏聞（そうもん）すべきことを書き，仕出すこともありしなり。
－－
あれこれ調べると，笏の使い道については，上と同様，メモ書きということになっています。
ですが，この『江家次第』には，上の文の前に，もう１文書かれています。
－－
笏は身の真中に有るように持ちて我が身のひずみを直すべき為の定矩なり。
－－
『江家次第』が記されたのは，平安後期。
当時の正座は安座。つまりあぐらですから，今の正座に比べ体がぐねりやすいです。
ぐねってしまう体を，平安貴族は笏を使って時々まっすぐに直していたのです。
また，『貞丈雑記』には，笏の作法が記されています。
－－
公家にては礼儀を正して物を申さるる時は，左右の手にて笏を持ちてむねのまん中の通りに持ちて礼儀を申さるるなり。
－－
礼儀正しく話すときは，笏を体の中央にセットしていました。
体と笏の「中央揃え」ですね。
上体も笏も縦にまっすぐ。こうすることが礼儀正しい姿だったのです。
姿勢を良くすることは，平安時代から行われていた作法です。
１０００年以上も続いている，日本古来の伝統的作法なのです。
私の友達には姿勢の良い人が多いです。それが嬉しいです。
－－
関連記事：
Ｎママから，また，話を聞くことが出来ました。
入学前のお子さんに，算数クラウドを少しずつ使わせています。
クラウドを見せたら，お子さんは「６年生のをやりたい」と言い出したそうです。
こういう気持ちが素直な学習の気持ちです。
どの学年を教えていても，「これは上の学年の内容だよ」と言うと，子ども達はとても燃えてきます。
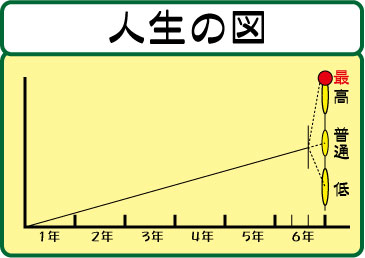
この気持ちをぐっと抑えさせて，３年生の棒グラフのソフトを見せたそうです。
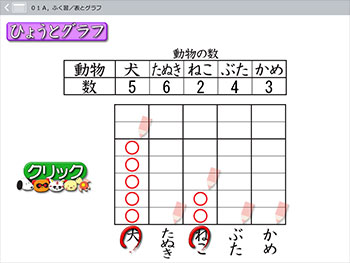
棒グラフのソフトの１番目は「０１Ａ，ふく習／表とグラフ」です。
２年生で習ったグラフをまず復習するところから，３年の棒グラフはスタートしています。
このソフトを見たお子さん。
最初はとまどっていましたが，○がどこまでつくか，すぐに分かるようになったそうです。
グラフの縦軸の意味合いが，つかめたのですね。
棒グラフは，数直線を複数並べた物ととらえることが出来ます。
ですので，同時に数直線の理解も進んだことになります。
入学前から，算数的体験を重ねるのですから，入学する頃がたのしみです。
－－
★３年生の棒グラフ，これがわからないと全滅
カンボジアに行くことになりそうと思っていたのですが，もう，乗る飛行機が決まっていました。
ミッドナイト発の飛行機に乗って，タイのバンコクへ行きます。バンコクで乗り換えて，カンボジアに入ります。
飛行機の行き先は，シェムリアップです。
アンコールワットの有るところだそうです。
アンコールワットはとても有名ですが，それがいったい何なのか，まったく知りません。ウキを読んだのですが，今ひとつ，ぴんと来ません。
バンコクに行って，何をするのか，ざっくりと教えてもらいました。
「算数ソフトの話したり」「算数ソフトを使って授業をしたり」
そういうことですと，聞いています。
どんな話でも，言葉が通じなくても，算数なら大丈夫です。
アラビア数字は世界共通ですし，小数点も共通です。
面積だって，体積だって，共通です。
算数は国際的概念！とつくづく思います。
－－
もしかしたら，この秋も，「奇跡の算数セミナー」が東京で開催できるかもしれません。
目下，工藤先生，佐藤先生からお話がいただけるので，適当な会場があったら，開催したいと考えています。
開催する場合は，１１月２２日（土）です。
そのときには，カンボジアの話もできると思います。
関心のある先生，決定したら，ぜひ，お申し込み下さい。
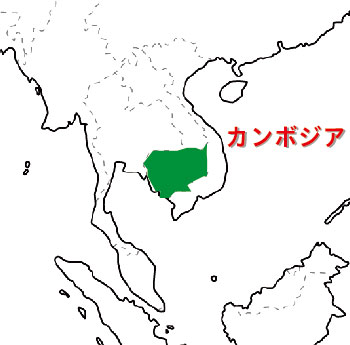どうも，カンボジアに行くことになりそうです。
まだ，詳しいことは何も聞いていないのですが，そういう話が進んでいるようなのです。
一言知らされただけですが，もし，そういうことになったらと思い，カンボジアをちょっとだけ調べました。
アンコールワットが有名で，仏教国。
この時点で，持って行く本は，聖徳太子の『三経義疏（さんきょうぎしょ）』当たりにするかと，思っています。
でも，出来ればしっかり読み返して，事前学習をしてから，現地に行くのがモアベターではないかと，ふつと思いました。
タイは仏歴が使われているようです。
仏歴は紀元前５４４年の釈迦が入滅した年が紀元となるのですが，タイは１年後の紀元前５４３年が紀元となっているそうです。
今年はタイ仏歴２５５７年です。
日本の皇紀は紀元前６６０年ですから，今年は皇紀２６７４年となります。
キリストの紀元はキリストが生まれた年。
仏歴は，釈迦が亡くなった年。
皇紀は神武天皇が即位した年。
それそれ，考えがあるのでしょうね。
野口先生と，昨年，ベトナムへ行きました。
カンボジアは，ベトナムの西隣の国です。
ということは，その次は，さらに西隣のタイかもしれません。
もし，そうなったら山田長政を事前学習してから行きたいと思います。
－－
教育書や児童書を出している老舗，星の環会の栗山社長さんと一献傾けました。
ちょっとした展示会があり，栗山社長さんがそこに来てくれました。
あれこれ話して，その日の夜に星の環会の会社を尋ねることになりました。
こういうケースは，非常に珍しいです。
星の環会の会社に入って，びっくり。
社内に，歓談できる大きな長いテーブルがあるのです。
すぐそばには，対面式のキッチンまで。
ここは，本当に出版社なのだろうかと，ちょっと思いましたが，周囲は本本本・・・です。
いろいろな話をしたのですが，星の環会さんから本を出していて，さくら社からも本を出している宮内主斗先生の話になったとき，やっぱり，嬉しいものがありました。
宮内先生は，理科の造詣が深く，人物もグッド。そんな話をして，盛り上がっていました。
宮内先生は若い頃から，理科一筋のような先生です。
論文もたくさん書いていますし，本もたくさん出しています。
自分たちで主催したセミナーに講師でお招きしたこともあります。
動物の頭蓋骨など，実物を持ってきてくれ，
話す内容は根本的なところからはじまります。
本格的な理科の先生だと，つくづく思ったものでした。
野呂先生の話題もありました。
理科実験の神様みたいな先生で，世の中には本当に卓越した先生がいると，痛感しています。
－－
