東京で用事があり，その道中，『木簡から古代が見える』の続きを読みました。
自分の知りたい内容は書いていないと分かったのですが，妙に，面白く最後まで読みました。
そうしたら，グイッと来る良い感じのことが乗っていました。
本は，やっぱりいいですね。
論語が記されている木簡。日本のみならず，朝鮮半島や中国でも発見されているそうです。
木簡に書いてあるので，それをなんと，「虫食いパズル」のやり方でテストをしていたと載っていたのです。
論語とか経書のある一行だけを見えるようにして，さらに，その一行の中の３つの漢字に紙を貼り付けます。
その紙を貼った所には，どんな文字が書いてあるのか当てさせるテストがあったそうなのです。
こういうテスト，今も，穴あき問題とか，虫食い問題と言われ継承されています。
また，算数の指導でも，虫食いはかなり重要な指導法です。
算数の特質を考えて，虫食いを使うと，広がりのある質の高い授業が出来ます。
私にとって，かなり関心の高い虫食いのルーツが，どうも中国の科挙で使った木簡となるようなのです。
科挙につながったこの一点で，実に有意義な本になりました。
科挙の該当部分の載った文献を読みたいのですが，ちょっとこの本からでは追跡できません。
もう一冊，『飛鳥の木簡』という本も買ってあるので，そちらも読んでみようと思います。
『続日本紀』を読んでいたら，突然，木簡には何が書かれていたのか気になり，続日本紀がまだ途中だというのに，『木簡から古代が見える』を購入しました。
半分ぐらいまで読み進めていますが，面白いです。私の知りたいことは何も書いてないことが分かりましたが，それでも面白いのは，平安初期の頃の都の様子や物流の様子などが書いてあるからです。
横道にそれつつも，『続日本紀』を少しずつ読んでいます。
今日は，岩波の新日本古典文学大系の『続日本紀一』が届いたので，早速，気になるところを探して，どのように記されていたのか調べました。
そうしたら，読み下し文が実にいい文章で，平安の世の日本語の響きを生で聞いているような気持ちになりました。意味は分かりにくいですが，読み心地はいいです。
気になっていたことの一つは，法要の初七日とか四十九日という表現です。お葬式になどで，「七七日」という書き方を見ることがあるので，これがいったいいつ頃から使われていたのか，気になっていました。
そうしたら，現代語訳に「初七日」「七七日」とあったのです。原文でもそのように書いてあるのかどうか，気になり，確認したかったのです。
調べてみたら，キチンとそのように書いてありました。
特に嬉しかったのは，持統天皇が死去されてから７００日後に当たる日に，「百七斎（ひゃくしちのさい）」と記されていたことです。
持統天皇ですから，奈良時代に入るちょっと前の天皇です。飛鳥時代の末期には，仏教の法要が貴族の間に浸透していたのです。
結構面白いところまで進んだので，国史大辞典で七七斎を調べてみました。
そうしたら，続日本紀がその初見と書いてありました。これより，昔のことは，中国の魏書となるそうです。
初七日などは，法華経にも書いてなかったように思うので，どういう経緯でこういう儀式が生まれたのかも気になりますが，出所が中国の魏の時代となっては，これ以上は追うことが出来そうにありません。
きっと，誰か考えついた人がいたのでしょうね。
たぶん，葬儀はいろいろと大変だったので，それを簡略する方向で七日に１度という形が作られたのではなかろうかと，私は思っています。でも，どうして７日毎なのか，それも気になります。
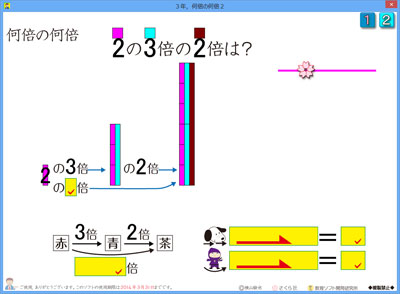藤本先生からありがたいメールをいただき，３年生の「何倍の何倍」のシンプルソフトを作っています。
シンプルソフトというのは，余計な要素を取り去って，骨格だけを学ぶソフトです。
見ればおわかりいただけると思いますが，３倍の２倍は６倍なんだということをキッチリと頭にれてもらうソフトです。
こういう基本が頭に入れば，後は適応です。数問，具体的な問題を解けば，場面理解が出来ます。
レベル２は，何倍の何倍のトックンです。
「→→」で計算した方がいいのか，「－→で」一気に計算した方がいいのか，出てきた数に応じて，判断していけばいいことを体験的に学習できます。
そういうことへの意識付けとなるように，レベル１の犬と忍者の絵柄に矢印を付けました。
－－
この学習でもそうですが，「２の３倍の２倍」を１問解いただけ終わりにしたら，確実に理解不足の子がでてきます。
最低でも３問は類題を解かないと，確実な理解には結びつきません。
１問目，２問目は，面食らう所もあるので，少々ゆっくり進めます。
そうして，３問目，４問目で気付く子が増えてくるので，次第に加速が付いてきます。
これって，ジェットコースターのスタートに似ていますね。
自分なりに考えるので，だんだんきまりが分かってきます。
「あっ！そうか！」と思った途端，ゴーーッ！と加速します。
こういう算数ソフトを使う授業を受けられる子は，幸せですね。
明日も算数をやりたいという気持ちでいっぱいになります。
嬉しいことです。
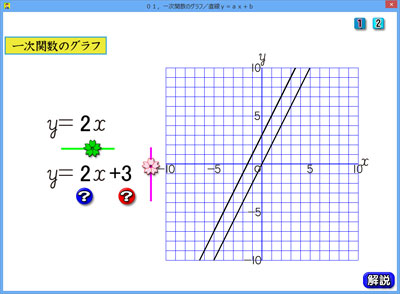中学２年の数学，一次関数のグラフのソフトです。
式とグラフが，実は同じ内容を全く違う見せ方で見せているというのが関数の単元です。
こういう日常ではたとえを言いづらい世界が数学の世界にはあります。分かれば，実に驚く世界となります。
数学も算数と同様，すべて規則で成り立っています。
ですので，式とグラフの関係は，具体事例を複数みることで，あっという間に頭に入ります。
ソフトの作りです。
特に，説明を要しないと思いますが，桜スライダーを動かすと式の数値が変わり，グラフも同時に変わります。
ですので，あわてることなく，ちょっと動かしては，数とグラフとの関係を見るようにしていきます。
見ていれば，式とグラフの関係がグイグイ分かってきます。
そうは言っても，見当違いなところ所に目がいくこともあります。
そういう事があっても問題なく理解が出来るように，[？]ボタンを設置してあります。
[？]ボタンは視覚化するボタンです。
傾きと切片の意味が見えやすくなります。
『続日本紀』を読んでいます。
日本書紀の続編の正史です。
日本書紀も面白いですが，これも思っていた以上に面白いです。
まず，グッと来たのは博打はダメだったということです。
「博打や賭けごとをして，遊び暮らしている者を取り締まった。」
いわゆる遊び人は昔もダメだったのです。生活を崩すこともありますが，生産をしないでも過ごせることに甘んじるその精神の堕落が，世の中に悪影響を及ぼしていたのだろうと思います。
唐の人が見た日本人観も出ていました。
「唐人がわが使者に言うには『しばしば聞いたことだが，海の東に大倭国があり，君子国ともいい，人民は豊かで楽しんでおり，礼儀もよく行われているという。今，使者をみると，身じまいも大へん清らかである。本当に聞いていた通りである』」
魏志倭人伝にも，穏和で争いを好まず，礼儀正しい事が記されています。
相手を思いやる心，目上を大切にする心といった，日本人にとってはごく当たり前のことが珍しいのかもしれません。敬語と礼儀作法が高い水準で保たれているのは，国の大きな顛覆が無かったからだと思います。それが何よりありがたいと思います。
その礼についても，詔が下されたことが記されていました。
「そもそも礼というものは，天地の正しい法であり，人間の生活の手本である。道徳や仁義も礼によって初めて広まり，教訓や正しい風俗も礼がそなわることによって成就する。」
これは，まさに儒教です。仏教が広まっていた時代ですが，儒教を捨てずに仏教を吸収しようとしています。優れた新しい文化をこれまでの文化の中に上手に取り込んでいく日本人。たいしたものです。
途中まで読み進めて，どうしても，気になる言葉と遭遇しました。
今読んでいる本は現代語訳ですので，実際にどういう言葉で記されていたかは，よく分かりません。読み下し文が載っている本でその言葉を確認したいので，それを注文しました。
－－
中学２年の「一次関数とグラフ」のソフトを作りたいと思っています。比例を習った子が見たら，ナルホドと思えるぐらいのソフトになればと思っています。
入学前の子が使って勉強するソフトです。
昨日の続きです。
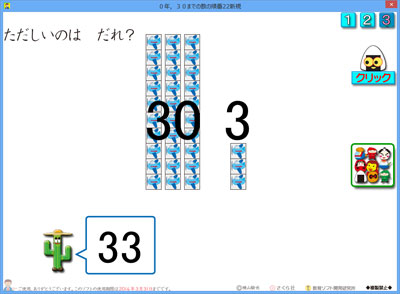
レベル３の画面です。
どっちが正しいか，自分で考えて，「サボテンだ！」と思い，サボテンをクリックした直後の画面が，右の画面です。
低学年を経験されたことのある先生なら，この画面を見て，「あっ！」と，ピンと来たと思います。
この後は，ご期待に沿った動きが始まります。
入学前の子がこのソフトを見て，ちょっと高めの算数学力が身についたら，それは良かったなとなります。
ＭＬで藤本先生も奥田先生が常々話してくださることは，それなりに「量をこなすこと」です。
ソフトの場合は，その量をこなすことが実に簡単にできます。
しかも，楽しいです。
最初，正答できなくても，何問かやっている内に，正答が分かってきます。正答になる「きまり」を理解する一瞬を迎えるからです。この一瞬を通過すると，次々に正答し続けるようになります。そうして，何回やっても必ず正解できるようになったら，押さえで「３回連続正解」にチャレンジします。３回連続して正解できる。これが，「きまり」が頭にしっかり入ったと判断していいレベルに到達している証となります。
日を置いて，またやってみてます。
簡単なので，すぐに終わってしまいます。
こうして日を置いてやっても，問題なくできれば，それは確実にマスターしたレベルとなります。体に染み込んだレベルですね。
このソフト，もうすぐ大方出来そうです。
ＭＬの先生方に見ていただこうと思っています。
