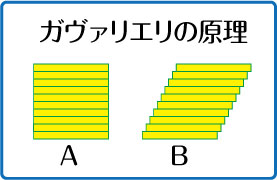
同じ長さの細長い板を10枚ずつならべています。
Aは真っ直ぐに並べていますが,Bはちょっとずつずらして並べています。
さて,どちらの面積の方が広いのでしょうか。
このように問われても,どちらかが広いとは思えません。広さは,重なってさえいなければ,並べ方によって左右されないからです。
ガリレオ(1564~1642)の高弟だった,17世紀のイタリアの数学者ガヴァリエリ(1598~1647)は,それまでの数学の考えを進め,「面は幅のない線の集合」と考え『不可分量の幾何学』にまとめました。
この考え方は,頭が柔軟になります。Aのカチッとした面積が自由自在に動き出すような気持ちになってくるからです。
ですので,『不可分量の幾何学』には,いったいどんな風に書いてあるのか気になります。読んでみたいと思うのですが,こういう本の翻訳本があるのかどうか,それすら分かりません。
今,小学校で教えている方法は,面積を辺でがっちり固定して見る方法です。ですので,見た通りにしか図形が見えてこない頭になっていきます。これは,教える先生も同じです。
これをガヴァリエリのように,積み重ねているという形でも扱うようになったら,高さが同じなら途中はどんな状態でも関係ないことがわかります。自由にスライドさせてもかまわないと頭が働くようになります。
こういうソフトを,いつかつくって,面積の発展的な見方として見てもらえたら良いなぁと思っています。しばらくは,作れませんが・・・。

![キーワードでひく小学校通知表所見辞典[増補版] -2057文例◎ぱっと開いてすぐ書ける- CD-ROM付](http://www.kennya.jp/app-def/S-102/kennya/wp-content/uploads/2014/08/76-8.png)















