点対称の２本目のソフトをつくっています。
親友の奥田先生から「頭ではわかっていても、目が慣れるまで時間がかかる」のが点対称とアドバイスをいただきました。
ありがたいです。１０年ぶりに復活した「対称の図形」。アドバイスのおかげで，過去の授業の光景が浮かんできました。ソフト開発にも元気をいただきました。
点対称の図形を書くとき，「頂点→中心→解答点」という目が働かないと，正しく作図できません。そこで，そういう補助線が出るように，ソフトを作り込んでいます。
完成したら，「もっと算数」にアップしますので，初めて点対称を指導される６年の先生，ぜひぜひ，ご活用ください。大先輩の奥田先生のアドバイスが効いているソフトです。授業の役に立ちますよ。
すでにアップされている，線対称のソフトを，城ヶ崎先生が授業で使いました。
その授業の話を伺ったのですが，「さすが！」の連発でした。
作図操作は子どもがマウスで行います。みんなが見ている中，マウスを動かすのですから，多少なりとも緊張します。マウスの動きがぎこちないとき，他の子は「違う，違う，こっち！」などと「日常の言葉」が次々出てきたそうです。
これを聞いて，「なんともったいない」と思った城ヶ崎先生は，「算数の言葉」を使うように指導しました。
「上」「右」「対称の軸」，数
これで子ども達の言い方が，より具体的になり，伝わりも良くなったとのことです。
学習の雰囲気もグッと良くなったのだなと，話を聞きながら思いました。
算数ソフトを使うと，指導者にゆとりが出てきます。言葉の指導などもソフトを使っているときにどんどん進めていくと，他の授業でもそれが生きてきますね。
これも，新しい算数指導の一つの姿です。
千葉大学の大田先生の研究室におじゃましたとき，紹介してもらった１冊が，『アメリカ流 ７歳からの微分積分』（ドナルド・コーエン）です。
正直なところ，この教え方は数学者でないと出来ない方法です。ですが，算数・数学の考える力をいっそう伸ばす考え方が，この本には記されています。
たとえば，次のように書いてあります。
「問題を解くには，パターンをまずさがしてみることです」
同様のことは，元筑波大付属小の正木孝昌先生も『算数の授業で教えてはいけないこと，教えなくてはいけないこと』で，「算数的な見方をどうのように教えるか」「きまりを見つける経験をさせる授業」と，記しています。
コーエン先生は，「何が起こっているか，どういう仕組みになっているか，理解をすることです」と続けています。
これが，「はじめに」に書いてあるのです。洋の東西を問わず，算数・数学で大切なことは，「きまりを見つける」事なんだと，再認識できました。
コーエン先生のこの本は，いきなり，無限級数の話から始まります。かなり，くじけそうになりますが，これがわかりやすいのです。大筋の考え方が，読み進めていると分かってきます。
個人的に，ちょっと嬉しかったのは，所々に出てくるベーシックのプログラムを，ディレクターだったら，こう書くのかなと，プログラム言語変換ができたことです。ですので，事例として示されているいくつかを，いつの日にか，ソフトとして作ってみるのも楽しいだろうなと思いました。
城ヶ崎先生や佐々木先生と話している算数ソフトの授業も，算数的きまりを子どもが見つけ出していく授業なのです。どんどん理解できるのは，「決まりを自分で見いだしている」からなのだと，強く感じます。
ここから，一歩踏み出すこともできそうです。ソフトできまり見つけに慣れた子は，「算数の問題を見たとき，パターンを見いだそうとする子に育つのではないか」と，コーエン先生の本を読んで思いました。
算数ソフトを使った授業を通して，たくさんの研究が出来そうです。嬉しい限りです。
展開図を見て，体積を求めるソフトです。
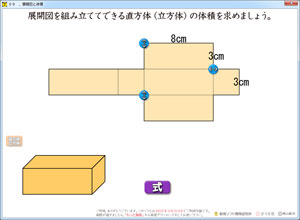
あれこれ考えて，展開図のサイズを変更できるように作りました。
変更の仕方は，とても簡単です。マウスで，スライダーをドラッグするだけです。これだけの操作で，展開図のサイズが長くなったり短くなったりと，変わっていきます。
展開図のサイズが変わるだけでも，十分に算数的なのですが，今回は，これに「連動する立体」をセットしました。
展開図の縦が長くなれば，立体の縦も長くなります。プログラムが出来，実際に操作してみると，これが良い感じなのです。面白いのです。立体が細長くなったとき，自分で「へー！」と言っていました。
５年生の先生，このソフトも「もっと！算数」にアップします。どうぞ，ご活用ください。
－－－
「算数数学好きを増やす会」のメーリングリストで，奥田先生が算数ソフトと連動したプリントをご紹介くださいました。ＰＤＦです。５年生の先生方のお役に立つと思いますので，リンク先をご紹介します。
http://www.geocities.jp/y_okkuu/genki/s509-02.pdf
「ソフト」と「プリント」の連動が，奥田先生の手でついに始まりました。
少しずつですが，新しい算数が動き出しているように感じています。
日本国中の子ども達が算数好きになりますように！
５年で「平均」を学びます。
この単元は，新しい概念として「平均」を初めて学ぶ単元です。
こういう「未知」の概念を学ぶときは，出来るだけ，イメージを示した方が良いです。
このイメージを，言葉でつかませるか，視覚的につかませるかは，先生方が決めていくことですが，算数は抽象への道を突き進む学問なので，言葉より，出来るだけ視覚的につかませる方が良いです。それも，動的な視覚化がグッドとなります。
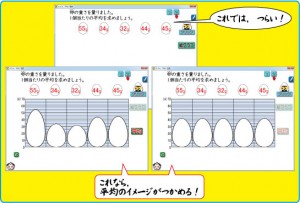
５年の１巻に入っている「平均」では，たとえば，上のように卵のイメージ図が登場します。卵の重さが，卵の高さに切り替わってグラフ化されています。棒グラフが卵になったものです。
この卵の高さが，クリックすると，ジワーッと平均化されるように，動きます。
これを何度か見せると，子ども達は平均がどんな概念なのか，感覚として分かるようになります。
数学の入門書を時々読んでいます。
入門書といえども，数学です。算数とは段違いに難しいです。
そんな難しいページにさしかかったとき，読者としての私は，そこで挫折することもあれば，何とか先へ進めることもあります。
昔は，私の力量の無さによって，そうなっているだと思っていました。でも，最近は，「著者の教え魂」に関わっていると感じています。
本気で，本の内容を，数学がイマイチの読者に分からせようとしている著者の本は，何かしらイメージしやすいように工夫がされています。先日，おじゃまをした大田邦郎先生の数学の本はその典型です。
クラスの気になるあの子が，「先生，平均って，こういうことでしょ！」と，嬉しそうに自分なりの言葉や，ジェスチャーで説明をしてくれたら，それは先生の「教え魂」がとってもグッドだったのです。
６年の「分数のかけ算」で，城ヶ崎滋雄先生が，効果のある新しい指導法を実践中です。
新しい指導法というのは，見て学ぶ学習法です。とりあえず，「見学学習」と呼んでおきます。
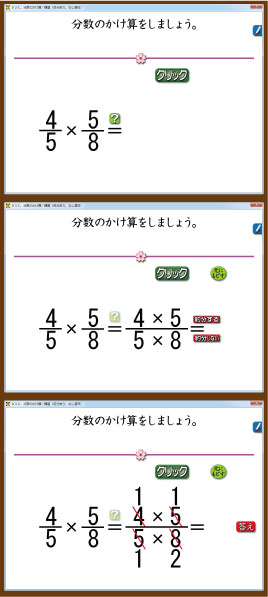
どのような学習かというと，「分数のかけ算」の一連の流れを，口頭で答えさせる学習です。「５かける８分の４かける５。約分して，２分の１」という具合です。
使ったソフトは，算数ソフト（さくら社の算数ソフト６年４巻）です。[クリック]ボタンをクリックすると，分数のかけ算が出題されます。[？]ボタンをクリックすると，長い分数が登場し，約分をするのかしないのか，問われるます。正しい方を選び，クリックし，答えにたどり着きます。
これを，教室の端にいる子から順に口頭で答えさせ，トータル３０問ほど見て学ぶ「見学学習」をしました。その後，教科書とドリルの練習問題をさせたら，全員の子が正しくできいたのです。
たくさんの量を見て学ぶ「見学学習」は，佐々木智光先生も，３年生の九九のきまりの単元で「７×（ ）＝２８」という問題に答えさせる場面で，実践されていました。こちらは即答できるので，トータル３００問も行い，全員が完全に出来るようになったのです。
佐々木先生の先行実践もあったので，城ヶ崎先生は，こういう練習場面はノートに書いているより，口頭でどんどん答えさせ，量をこなす方が子どもの頭に良いと感想を語っていました。
算数ソフトを使うことで，こういう新しい指導法が生まれてきていますが，特別な難しい指導法ではありません。「ここの学習なら口頭でどんどんいける」と思ったところを，そのように指導すればいいのです。それで，成果が上がるのです。嬉しいことです。
分数のかけ算の計算手順には，一定のきまりがあります。数問繰り返して「見学学習」をすると，そのきまりが見えてきます。しかも，誰かに教えられて分かるのではなく，自分からきまりを見つけ出すのです。ここが，斬新な指導なのです。
自分で決まりを見いだしたとき，そのときこそが「数理的発見」をしたときなのです。それをさらに何問か解くことで，「自分の発見が確信」へと高まり，「定着」するのです。嬉しい瞬間が連続してやってきます。
これが，誰の頭にもやってくるように授業できるのが，「見学学習」です。先生にとっても嬉しい嬉しい授業になりますよね。皆さんのクラスでも，ぜひ，城ヶ崎先生や佐々木先生が行っている「見学学習」をやってみてください。
※ 城ヶ崎滋雄先生がブログを開設しました。「城さんの、それもまた良し」です。
http://jyo12345.blog97.fc2.com/
是非，ご覧ください。
小学校で習うグラフは，昨年度までは次の４つでした。
棒グラフ
折れ線グラフ
帯グラフ
円グラフ
これに，新しく今年度から次のグラフが登場します。
柱状グラフ
昔の算数に登場していた「柱状グラフ」が帰ってきたのです。
合計５つのグラフを学ぶのですが，それぞれの特徴をざっくりと把握していると，指導の味が少し変わってきます。
棒グラフは，多い少ないがわかりやすいグラフです。
折れ線グラフは，変化がわかりやすいグラフです。
帯・円グラフは，全体のどれくらいかという割合がわかりやすいグラフです。
そうして，柱状グラフです。
これは，いったい何がわかりやすいのでしょう。
こういうグラフの特徴がわかると，調べたことをグラフ化する時，どのグラフで表したら効果的かがわかります。伝わりやすい「見せ方」ができるのです。
たとえば，「お小遣い」をテーマにしても，どのグラフが良いか，状況によって決まってきます。
友達との違いを見るなら，棒グラフです。
小さいときからのお小遣いの推移なら，折れ線グラフです。
今月のお小遣いを何にどれだけ使ったかなら，帯や円グラフです。
グラフ選びは，伝え方技術の一つなのです。
小学校の授業では，グラフを選んで伝え方を考える所まで進みませんが，社会などとの関連でグラフ化したい時に，こういった算数の考えが役に立ちます。
柱状グラフ。これは，「さくら算数ソフト」６年５巻に入っています。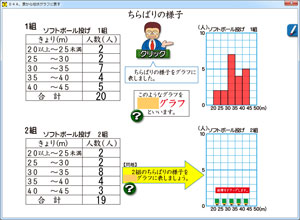
右のソフトは，表から柱状グラフに変換するところを学ぶソフトです。上の表とグラフがお手本で，下は実際にマウス操作で柱状グラフの「柱」づくりが出来るようになっています。
もちろん，クリックすれば，何回でも繰り返し勉強できます。
柱状グラフで難しいのは，柱の「範囲」にどのデータが入るか，というところです。そこの所もソフトには収録されているので，動きを見れば，「なるほど！」がやってきます。
一つ一つの柱に入っている人数を高さで示すことで，「分布」が分かりやすくなります。身近なところでは，テストの点数も，１０点刻みで範囲をもうけ，その中に何人はいるかを柱状グラフにすると，そのテストの傾向が見えてきます。
グラフとして学ぶのは５種類なのですが，実は，数直線もグラフの一種です。文章問題に出てくるテープ図や線分図もグラフの一種といえます。数を配置することで，見えやすく，わかりやすくしているのです。テープ図や線分図を文章題で用いるのは，数を配置することにより，どういう計算になるかを考える思考の場所にしているのです。このあたりのことについては，文章題の話題の折りに書いていきます。
日常の指導も，グラフのように「見える」ようにすることで，伝わりが良くなります。
「あなたの話の中身が見えてきた」「君の話はよく見えない」という言葉から始まっているのが左の山本正実先生の『伝わる伝わる見える指導』です。
指導のキーワードは「見える」
具体的な物とつながると「見える」
指導力も伸ばす「見える」指導
と，グッと来る話が書いてあります。
私が算数のソフトを作り続けているのも，この「見える」の考え方の流れに乗っています。
ソフトでは，算数の動きが「見える」から，伝わる指導になるのです。
