「第２回 奇跡の算数セミナー」を７月２７日（土）に開催します。
会場として，水道橋駅近くの会議場をお借りしました。
２０名で満員となる部屋を借りましたが，ＰＣなどを設置しますので，どう考えても１８名様までの入室となりそうです。
ベトナムへ行く前に，kyositu.comニュースやフェイスブックでお知らせしました。
早速，参加希望のメールが届き，残席はわずかに４席となりました。
参加ご希望の先生，御連絡をお急ぎください。
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
第２回 奇跡の算数セミナー
～「見れば分かる算数」からの出発～
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
遅れると取り戻しが難しい算数。
その算数に，今，異変が起こっています。
手を挙げることの無かったあの子が，急に手を挙げはじめた。
「明日も算数ある？」と，算数を楽しみにする子が出た。
遅れていた子が，「見ている内に分かった！」と言い出す現象が起
こっているのです。
しかも，ある日１日だけそうなるのではありません。
毎日のように続きます。
このような授業はどのようにして生まれるのか。
それから，どう指導を進めたらよいのか。
「第２回 奇跡の算数セミナー」では，その実践やヒントを提案し
ます。
──────────────────────────────
※日程や内容は変更になることがあります。
１ 日時
７月２７日（土）１４：００～１８：００
２ 場所
内海（うつみ）３Ｆ
東京都千代田区三崎町3-6-15
http://www.kaigishitsu.co.jp/
３ 参加可能人数
１８名限定
４ 日程
13:30~ 受付
14:00~14:10
趣旨説明————————–
14:10~14:30
第１講座 理論編
「子どもが算数を理解するということ」—-横山験也（千
14:30~16:50
第２講座 実践編
「見ているだけで力が付く算数指導１ 回数にこだわれ！」
————–佐々木智光（千葉県）
「見ているだけで力が付く算数指導２ 力の向け所はここだ！
————–城ヶ崎滋雄（千葉県）
「複式学級で実現した自学自習システム／その準備と計画」
—————-奥田吉彦（和歌山県）
「学力向上推進教員のデジタルとアナログの融合指導」
—————-藤本浩行（山口県）
「Ｕ３０が巻き起こす，マネジメント式算数指導」
————–佐藤宗巧（神奈川県）
17:00~17:30
第３講座 算数ソフト最前線
「２学期に向かってＧＯ！」—————
17:30~
閉会—————————-
５ 参加費
２０００円
６ 申込先
横山験也 yo◆kennya.jp （◆を小文字の@に
（以下を電子メールでお知らせください）
１参加者氏名：
２勤 務 校：
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
明日からベトナムです。研究や研修ではありません。ツアーの観光旅行です。
誘ってくださったのは野口芳宏先生です。
ですので，中身はかなり濃くなります。
その前日の今日，ディレクターの３Ｄについて，プロの方とお話ししました。
どうも，算数の立体には良い感じのようなのです。
赤青の３Ｄメガネを掛ければ，そこに良い感じで立体が登場するようなのです。
その３Ｄメガネですが，紙製なら１００円ぐらいで手に入ります。
もしかしたら，立体の授業中に３Ｄメガネを掛けて「オーッ！」と声を出しながら授業をするクラスも出てくるかもしれません。
それを研究授業でやったら，参観された先生方も，子ども達より３Ｄ立体に目を奪われるかもしれません。
２０００年前後の頃から，こういう近未来的な授業がいつかできる日が来ると思っていました。
また，そういう授業に，強いあこがれを持っていました。
なぜなら，算数そのものの魅力で，子どもたちを魅了できるからです。
元来，算数は魅力の固まりのような教科なのですが，紙や黒板に描くという形でしか示せなかったので，その魅力が９０％ぐらい眠ったままなのです。
ソフトを作ることで，算数の魅力をかなり発揮できるようにはなったのですが，まだ，７０％ぐらいは寝ていると思っています。まだまだ多いに研究の余地があります。
どうやら算数は進化を始めたようだと考えるぐらいがちょうどよいですね。
校内研の通年の講師を引き受けています。
その小学校へ行ってきました。
今回は，「算数ソフトの紹介」です。
『子どもが夢中で手を挙げる算数の授業』全３０巻の中から，適時選び，どんなソフトがあるのか，紹介しました。
そうして，最後の１０分ほどは各学年で自由にソフトを見ていただきました。
今回の校内研，たぶん，全国的にも珍しい形と思います。
授業で使いたいソフトがなかったら，私の方でできるだけ準備していくという形で進むからです。
指導をする先生と，教材を開発する人とが力を合わせる感じの校内研になります。
この形は，今，算数好きにするＭＬで藤本先生や奥田先生達と実際に行っています。
それを校内研でも体験できます。
私にとっても，ありがたい研究となります。
帰り際，６年の先生と６月に授業するところを話し合いました。
「倍と割合」の所になりそうです。
指導案検討の日が近いようなので，早めにソフト開発をしてみたいと思っています。
ほるぷ出版の「３Ｄ 日本地図めいろ」が来月発売になります。
児童書をたくさん手がけてきましたが，３Ｄは今回が初めてです。
ですので，今，ちょっと３Ｄがマイブームになっています。
いままで気にもしていなかったのですが，ディレクター１２のサイトを見て，ビックリしました。
「高度な３Ｄゲームの制作」とドーンと書かれているのです。
これまでも，何度かディレクターのサイトを見てはいたのですが，３Ｄへの興味がなかったので，ずっとスルーしていました。
ネットで調べたら，どうも，紙の赤青の３Ｄメガネでも立体視ができるようなのです。
見るための３Ｄメガネは簡単に手にはいるとして，作るのは難しいのだろうなと思います。
それも，アドビのサイトに出ていました。
どうも，「_movie.stereoscopyParallaxDiff=20」と命令を書き込む程度のことで，奥行きが設定されるようなのです。
もし，これだけでＯＫなら，これは簡単です。
この２０をちょっと操れば，出てきたり引っ込んだりと自由自在です。
この出てきたときに，その飛びだし比率に合わせてズームアップするとなると，ちょっとやっかいですが，もし，そうだとしても１行か２行書き加えればいい程度ですみます。
もしかすると，「３Ｄ 学習ゲーム」「３Ｄ 学習パズル」が作れ，簡単に楽しめる日を迎えられそうです。
今はバタバタとしていて，そういうところのプログラムを勉強している余裕がないのですが，少し時間がとれたら，３Ｄのプログラムを組み立てて，試作第１号というのを発表してみたいです。
楽しみが増えて，嬉しい限りです。
東京駅近くにある丸ビルで酒席があったので，道中，『日本語（下）』を読んでいました。
本を読むスピードは，かなり遅いようです。
１冊読み終わるのに何日もかかります。急いで読むと，美味しいところを素通りするので，そんなもったいないことはできないと，頭が追い付くスピードで読んでいます。貧乏性なのかもしれません。
この本，日本語の本なのですが，下巻にも算数のことが載っていました。
分数です。
２／３を日本語では「３分の２」と下から上に読みますが，英語では「two thirds」と，上から下に読むのだそうです。
分数を上から下に読むようにしたら，縦書きの文章と同じ流れになるので，それはごく自然な読みの形になります。
そうなると，「２の３分」「２を３分」などという読み方になり，その意味がかなりつかみやすくなります。それだけでなく，２÷３にもつながりやすくなります。
金田一先生はそういう読み方にしたら・・と書いてくださっているのですが，算数の世界には届いていないようです。
もともと，分数は中国から輸入した概念です。
ですので，「三分之二」などと書いてある書物から学び，日本語として「三分の二」と読ませていました。
日本書紀にも，方丈記にも，江戸の書物にも中国学びの分数表記が登場しています。
そうして，明治になり，欧米の２／３という表記が輸入されました。すでに，読み方は中国流があるので，それをこの表記にバシッと当てはめたのです。
そうしたら・・・。なんと，下から上に読むことになったのです。
算術用語が決まっていくまでの間には，きっと，下から読んだら変だよ！という意見もあったと思います。
思い切って，欧米風に上から読もうといった声もあったろうと思いますが，当時の国内は「漢文崇拝」です。漢文では，返り点を使って下から上に読むのはごく当たり前のことです。違和感も少なかったので，いかんともしがたかったのだろうと思います。
はっきり分かったことは，読みは中国流，表記は欧米流というのが，今の分数の姿ということです。
この中洋折衷が下から読む原因なのです。
明日は，ひさしぶりに喫茶「さぼうる」で打ち合わせをするので，この本の続きを読みたいと思っています。
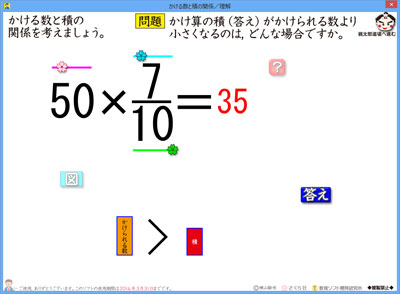１より小さい数でかけると，積は，元の数より小さくなります。５年生の時に，小数で勉強してきています。
同様のことが，分数でも起こるので，それを勉強するソフトを作っています。それが，ほぼ完成してきました。
「見ている内に分かる」アイデアが２つ盛り込まれています。
１つは，積が面積として大きくなったり，小さくなったりすることです。
これは見ているだけでも楽しいです。
直観的に，「そうか！」と伝わってきます。
２つめは，縦棒の長さでかけられる数と積とを見比べられるようにしています。
こう書いている内に，一つ機能を盛り込みたくなりました。
それを今，作り込みました。
ですので，ダウンロードできる時には，[？]ボタンが１つ増えています。
あると嬉しい機能を盛り込みました。
ダウンロード販売できるように，進めていきます！
－－
「見ている内に分かる」という状態が，どれほど子ども達を救えるか。
これは，算数ソフトを使う算数の授業の大きな研究課題です。
できない子へ，だれでも対応できる授業がそこに現れるからです。
最も重要なことは，見ている内に「何かに気付く」ことです。
こうでしょう，と教えられて分かるのではなく，自分で気付くことです。
この自分で気付く瞬間を迎えることこそが，算数の理解で最も重視する所です。
城ヶ崎先生は，４年生のわり算の筆算で，「九九のできない子」がわり算にチャレンジしてくる指導を展開しました。
もちろん，『子どもが夢中で手を挙げる算数の授業』の４年４巻を使ってのことです。
九九ができないので，わり算の筆算の「立てる－かける－ひく－おろす」の中の「たてる」だけをその子にどんどん答えてもらったそうです。
そうしたら，そこだけ注目すればいいので，次第に立てる数が分かってきたそうです。
その上，毎度，×１，×２，×３・・・と順に口にしていたのですが，途中から，×３から口に出すなど，「探索的思考」ができるようになったのです。
クラスの子も，その子を褒め・認めます。１時間の間に成長している姿に拍手を送ります。
親和的な良いクラスなのだと伝わってきます。
そうして，何倍を答えるテストをしたら，なんと６割も正答したそうです。
本人にやる気が出てきたので，伸びが始まったのです。嬉しいことです。
◆ 部分的に取り組む
◆ 集中して繰り返す
これが，「気付く」瞬間を迎えさせてくれます。
この瞬間がやってきたとき，「私もできるかも」を感じてきます。
すると，これまで算数に感じていた「暗さ」が，急に「明るさ」を持ち始めます。
「勉強したい」という気持ちが誘発されてきます。
その気持ちの流れに合わせて，導いてあげれば，伸びていきます。
