かけ算・わり算の線分図のソフトです。
まだまだ，開発途上です。
何を目的としているソフトかというと，線分図さえ正しく書ければ，その先の計算をどうやったらいいかは，特定のパターンで行えば良いということを学ぶソフトです。
学校でキチンと取り組む思考方法とちょっと違うので，好き嫌いが出ると思います。
しかしながら，この解き方は三数法というちょっと古い時代に真面目に皆さんが使っていた方法なので，あながち悪い方法ではありません。ある種，古典的なやり方です。
どういう風に計算をするかは，式を見ている内に気がつきます。
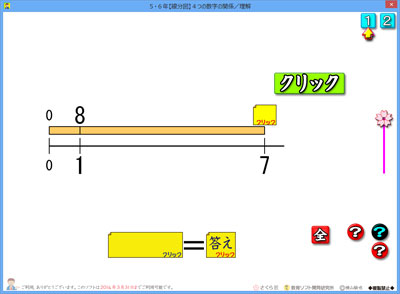
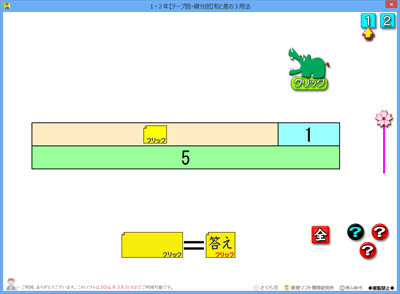
「斜めにかけて，残った数字で割る」
つまり，「７×５÷１」と行えばいいのです。
分からない数がどこにあっても，いつでもこの形になります。
右の場面では，残った数字が１なので，÷１はやる必要がないので，「７×５」で求められます。
どうして，「斜めにかけて，残った数字で割る」で求められるのかと，理由を考えると意識が飛びそうになります。
説明するには，座標を使わないとわかりにくいです。
ですので，そういうことは考えずに，数直線上に配置された４つの数字「１，７，５，？」の間に成り立っている数のきまりを元に，計算をしているのだと，理解します。
このレッスンをするだけでも，かけ算・わり算の文章問題への抵抗感はかなり小さくなります。
線分図さえ書ければ，確実に答えが出せると分かるからです。
慣れれば，線分図すらいらなくなります。ただ，２組の数字を書いて「斜めにかけて，残りを割る」を実行すればいいのです。
余談になりますが，この「１，７，５，？」は，文章にすると「１のとき７，では，５のときは？」というパズル感覚になります。
これにかけ算の意味を肉付けすると，文章問題になります。「１箱に７個ずつ，５箱では？」となります。
普通に考えた場合，単位量が出ていて，順思考の位置に？がある問題は，簡単に感じます。
逆思考になり，単位量の「１」が示されず，２や５になると，かなり難しいと感じます。
その難しさが，ウソのように消えていくのが，三数法です。
完成したソフトを見た先生の中には，レベル２から初めて，１の出る特殊な場合を後からやった方がいいなと感じる方もいると思います。そういう，摩訶不思議な世界が三数法の世界です。
－－
このソフト，数字を操るだけなので，かなり簡単に作れると思っていたのですが，予想を超えて厳しい道のりになっています。
でも，楽しいのでコツコツ前進させていきます。
友達の工藤先生が，昨日のブログをプリントされ，学校の先生方に配ってくれたそうです。
お役に立てて，うれしいです！
たし算・ひき算の文章問題の思考ツールとなる図のソフト。
一昨日，昨日と紹介しましたが，友達の先生方に喜ばれているのは，「桜スライダー」です。
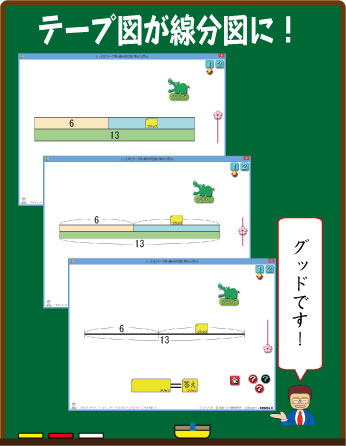
桜スライダーを下におろすと，テープがだんだん細くなります。
当然，中の数字は枠の中に入っていられなくなので，外に飛び出します。そのとき，寸法線もでてきます。
そうして，どんどん枠は細くなり，最後は１本の線になります。
たし算・ひき算の図は，大きく３つのタイプに分かれています。
１，テープ図（枠内に数字）
２，テープ図（枠外に数字）
３，線分図
できる子は，これらが「同じ意味」だと理解します。
しかし，今一歩の子は，「どれも別物」と理解します。
テープ図と線分図がつながらないのです。
ここをつなげたいと思ったら，やることはただ一つです。
口で説明するのではなく，「ウルトラマン理論」です。
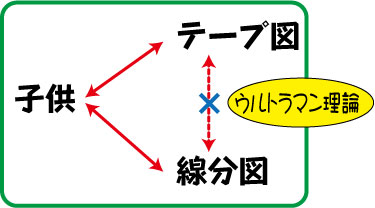「ウルトラマン理論」というのは，「説明すると難しいことを，見せることでパッとわからせる」，高級な理解理論です。
今回のように，２つの対象が同一であることを理解させるには，ウルトラマンのあの名場面を活かせばいいのです。
そうです。「変身」の様子です。
変身の様子を最初から最後まで見せてもらっているので，主人公とウルトラマンが同一人物だということを，子供でも理解できるのです。
これを，ナレーターが音声だけで変身しましたと言っても，変身という言葉の意味が通じません。変身の様子を見ていないので，納得感が無いのです。当然のように，保存もお粗末になります。
ところが，変身の様子を見ると，事態は一変します。スッキリわかります。
変身に非常に大きな無理があっても，現実にはあり得ないことだと分かっていても，変わる様子を見ているので納得感がでてきます。この番組ではこういうものなのだと，その世界に起こる当たり前のこととして納得していきます。
この納得感が，記憶の保存につながります。
ですので，テープ図と線分図も，その変身の様子を見ればいいのです。
これを一度見ておくと，納得し保存されます。
なお，ウルトラマンの変身は，非常に高級な論理を与えてくれています。
あの変身はウルトラマンになる様子だけを見せています。いわば，一方通行の動きです。
それでも，子供たちはドラマの終末には，元に戻ったと認識します。
これは，一方を見れば，あとは見た子が頭で「可逆性」を創り出すということです。
教材を作るときに，非常に役立ちます。
たし算・ひき算の図のソフトです。
昨日も紹介したソフトです。
今日は，「理解」ということについて，ちょっと書いていきます。
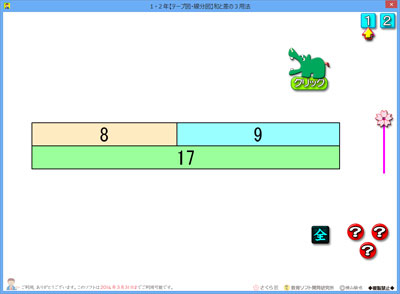
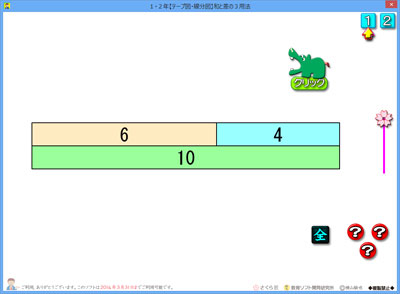
ソフトを起動すると，右のような画面が出てきます。
枠の中に数字が入っているので，何となく３つの数には何か関係がありそうな気がしてきます。
「上の２つをたすと下の数になる」と，スッと分かる子もいると思います。
しかしながら，違う関係に目をつける子もいて当然です。
「８→９」と数がつながっている。
１つ画面（１事例）で考えると，どっちも正しくなり，どっちの関係も素晴らしいことになります。
でも，授業では，たし算の関係の方が正しく，数の順番は否定されます。
１つの画面しか見ることができないと，否定された関係の扱いにも力を入れないとなりません。
「違います！」などと，上からドガンとやられたら，やる気を損なうことになります。
１つの画面を見る限りでは成り立っている関係だからです。
大事なことは，「最初に思いついた関係」「最初に気付いたきまり」は，確定した関係ではなく，一時的な「仮の関係」なのだと，理解することです。
そうして，その気付いた仮の関係の真偽を，自ら考えるようにすることが大切なのです。
何かしらの仮の関係に気付いた様子が見えたら，「クリック」ボタンをクリックします。
すると，２例目が出てきます。
これを見たら，「８→９」と「仮の関係」を創った子は，すぐに打ち消しを始めます。数が順番になっていないからです。
直ちに考えを改め，別の関係を探し始めます。
３例目，４例目と見る内に，たし算の関係になっていることに，容易に気がつきます。
－－
このような，
１．「仮の関係」の発見
２．自ら打ち消し・修正
３．「関係」の確信
という流れが，理解するという行為の原理です。
重要なのは，こういった理解が自分の頭で成されたとき，その理解は「保存」されるのです。
算数ソフトを使うと，学習が頭に残りやすいのは，この理解の手続きを踏んだ授業が簡単に行えるからです。
－－
このソフト，しばらくの間，もっと算数にアップしている予定です。
早めにダウンロードして御活用ください。
たし算，ひき算の文章問題の難関といえば，逆思考の問題です。
はじめに何個か持っていて，お兄さんから１個もらったので，全部で５個になりました。
はじめ，何個もっていたのでしょう。
こんな風な問題が，いわゆる逆思考と言われている問題です。
逆思考の場合，問題文を読んでもサッと式が浮かばないので，「図」をかいて，図から式を導き出すように取り組みます。
このソフトは，その「図→式」の部分だけを，レッスンするために作ったソフトです。
算数をしっかり勉強している先生は，こういうところに特別に時間をとって勉強をしますが，黒板やプリントで行うので，なんだかんだで１時間ぐらいはかかってしまいます。
それが，このソフトなら，たぶん１５分前後で，ほぼ全員理解できるようになると思っています。
朝自習などに，遊び感覚でやってみるぐらいで充分役立つと思います。
桜スライダーがついています。
これを下にドラッグすると，良い感じの現象が現れます。
ここがなかなか指導できなかった所です。それを「見れば分かる」指導ができるようになりました。
もっと算数にアップしますので，アップされましたら，早めにダウンロードして御活用ください。
３年生の「わり算を使う文章問題」です。
式を２つ使う文章問題なので，藤本先生はこれを「２段階」と話ししてくれています。
こういう意識を先生が持ったら，それを子ども達も感じ取れるように，指導ができるとグッドとなります。
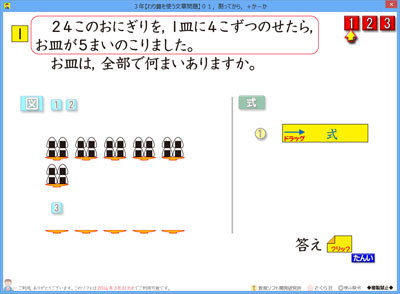
そこで，図でも式でも，２段階がくっきりするように配置しました。
もちろん，問題文の一部が図や式に飛び出すという，新方式をふんだんに用いています。
ソフトで飛び出す様子をしっかり見たら，その先のプリントなどでは，「ビューン」などといいながら「矢印」を使って解説をするといいです。「矢印」は動きをイメージさせる実に優れた方法だからです。
式の方では，カバーをドラッグしながら見せていくタイプにしてあります。
どんな式になるのか，ちょっとずつ見せながら授業を展開できます。
合計３問もプログラムしてあるので，見ているだけでかなり理解が進むと思っています。
近々，アップします。お楽しみに！
藤本先生から，嬉しいメールをいただきました。
子ども達が「わり算の答えを予想して、教室中が大盛況」となったのです。
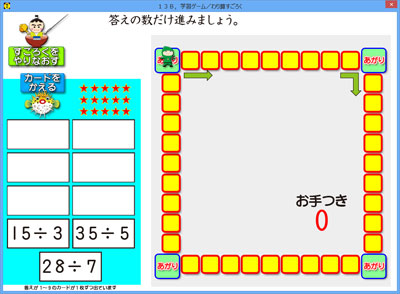
そうなった算数ソフトは，右の「１３Ｂ，学習ゲーム／わり算すごろく」です。
どんなソフトかというと，わり算カードを選んで，商の数だけ進むという双六です。
上がりは，４か所もあります。
ですので，簡単にあがれそうなのですが，それがなかなか思うようには上がれません。
９枚中３枚はわり算が見えていますが，６枚は見えないからです。
上がれそうで上がれない。これが子ども達を夢中にさせます。
大盛況になる，もう一つの理由は，ほとんどの場面が一発で上がれる位置になる双六だということです。
一発で上がれる位置にいれば，力が入ります。カード選びは非常に真剣になります。
自然と，見えている３つのわり算を真剣に計算してしまうのです。
双六中にカード変更（シャッフル）できるのも，わり算練習効果を高めています。
－－
このソフトは，『子どもが夢中で手を挙げる算数の授業』の３年４巻に入っています。
３年４巻には，「あまりのないわり算」と「あまりのあるわり算」のソフトが入っています。
授業に役立つソフトの他に，こういった大盛況となる学習ゲームソフトもちょこっと入っているのも，嬉しいところですね。
