Category Archives: 算数

ソロバンがバリバリにできる先生には，このソフトは無くても良いかなと思います。
それでも，２０人・３０人の子に教えるとなると，なかなか伝わりにくい所があるのがソロバンです。ソフトをお勧めします！

３年生の算数を教えていて，ソロバンがちょっと・・・という先生は，悩むことなく，このソフトです。
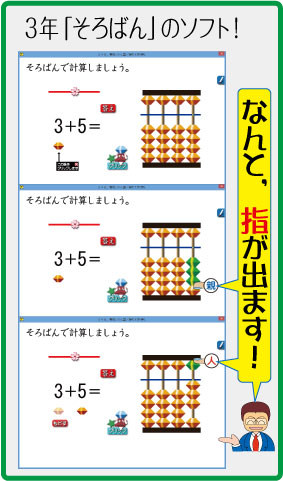
このソフトでは，ソロバンで計算する通りに，指が出てきます。画期的ですよ。指が出てくれるなんて！

下から上が「親指」で，上から下が「人差し指」で・・・。
ソフトを見ている内に，指運び（運指）に気付く子も出てきそうです。

ちょっと，ご説明しましょう。
このソフトは『子どもが夢中で手を挙げる算数の授業』の３年１巻に入っています。
３年の１巻には，「時刻・時間の計算」ソフトが２０本。「棒グラフ」ソフトが１５本。そうして，「そろばん」ソフトが１７本も入っています。
右のソフトは，「０４Ａ，整数／たし算／繰り上がり無し」です。
「繰り上がり無し」ですから，繰り上がりのない計算問題だけが出てきます。

「３＋５」と出ている「３」の下に珠（たま）がありますね。これにマウスを乗せると，ソロバンコーナーに親指が登場します。しかも，動かす珠が緑に変わります。
最初の「３」はこうするのか！と見ただけで，分かります。

珠をクリックすると，３は上に動きます。
そうして，「５」の下に，新しく珠が出てきます。
この珠にマウスを乗せると，今度は５珠の所に人差し指が出てきます。
何とはなく，下におろすような予感がします。
「どうなるでしょう？」などと，もっていくと，ワイワイ手が上がりそうです。

こんな風に，とにかく分かりやすく演出してくれます。
それが，マウス操作で簡単にできます。
ワイアレスマウスを使えば，子ども達も自席でクリックできます。
ソロバンが面白くてしょうがなくなりそうですね。
－－
「０４Ａ，整数／たし算／繰り上がり無し」の後には，次のようにソフトが入っています。
「０４Ｂ，整数／たし算／５へ繰り上がる」
「０４Ｃ，整数／たし算／十の位へ繰り上がる」
５珠に繰り上がるタイプ，上の位に繰り上がるタイプ。それらを別々に分かりやすく学ぶことができます。
もちろん，この後は，ひき算も出てきます。
－－
左がソロバンのソフトの入っている本の表紙です。
この表紙をめくると，ＤＶＤが出てきます。
それをパソコンのＤＶＤドライブに入れると，目次画面が出てきます。そこにファイル名が書いてあるので、それをクリックすると、ソフトが画面にドーンと登場します。
使い方は，とっても簡単です。

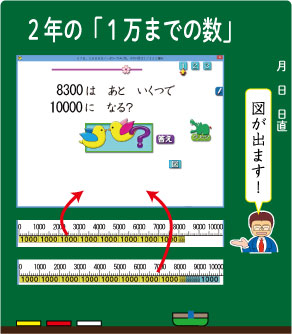２年生で学習する「１万までの数」。その中では、あといくつで１万になるかの勉強もします。数の補数を考える勉強です。
それをしっかり勉強できるようにと願って作ったのが、このソフトです。（『子どもが夢中で手を挙げる算数の授業』（２年３巻）に入っています）

カバのクリックボタンも用意してあります。こちらは、クリックすると問題がランダムに出てきます。考え方に慣れてきたら、「クリックボタンで練習」という学びができます。

このソフトの良いところは、図が出てくることです。
[図]ボタンをクリックすると、数直線と黄色いテープがでてきます。このテープは１０００単位のテープと、１００単位のテープで構成されています。ですので、大きな数の構造も一緒に学ぶことができます。
さらに、ボタンをクリックすると、青テープが出てきます。これが答えとなる数をあらわしています。

そうして、そうして。
この黄色と青のテープが出たまま、[桜]スライダーを動かすことができます。
スライダーの動きに合わせて、黄色・青のテープの境目が変化していきます。
問題文の数も同時に変わります。
それが、妙に面白いのです。興味を惹かれます。

こういうところが、算数のちょっと深い面白さなのだと思っています。

大分から戻り、メールを見ていたら、山口の藤本先生から、とてもうれしいメールが入っていました。

２年生のかけ算九九のきまりで使うソフトを使って授業をしたら、子供たちも担任の先生も大喜びされたそうです。

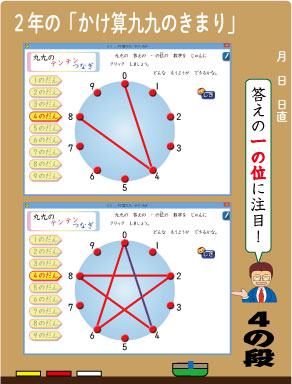
そのソフトというのは、右の画像のソフトです。『子どもが夢中で手を挙げる算数の授業』２年１巻に入っている「かけ算九九/点々つなぎ」というソフトです。

今、４の段の画像が出ていますが、４の段の答えの一の位の数を順にクリックしていきます。
４の段の場合、なんと星形になります。こういうのは、見ているだけでピリッと整っていて、きれいだなと感じます。
規則で成り立っているので、こういう左右対称のいい感じの図形になります。

規則で成り立っているといっても、「７の段は無理だろう」と思えてきます。
ところが、７の段をやってみると、妙に面白いことに気が付きます。
７の段の一の位の数は、３の段の場合の逆順で現れるのです。
これに気が付くと、あらあら・・・。
１の段の逆が９の段で、結果は同じ。
２の段の逆が８の段で、結果は同じ。
３の段の逆が７の段で、結果は同じ。
４の段の逆が６の段で、結果は同じ。

５の段で折り返すような感じで、「逆順で結果が同じ」になるペアになっているのです。
どうしてそうなるのかを考えてみるのも楽しいですね。

藤本先生は、ワイアレスマウスを子供たちに順次使わせ、赤いボタンをクリックしてもらったそうです。
これが、学級みんなでの共同作業のようになり、学級づくりとしても大いに役に立ったそうです。
算数の時間に学級の共同作業。ちょっと感動しました。

４年生では，「概数」を学びます。
「概（おおむ）ねの数」が概数ですから，平たく言うと，「およその数」となります。

ですので，概数では，たとえば，４６はおよそ何十と考えることができるか，というような勉強をしていきます。
このおよそで考えるときに，重宝するのが数直線です。
数直線を見ながら，４６は，およそ４０なのか，およそ５０なのか，どっちなのか考えるようにすると，理解が早まります。

このような学習で重要になってくる言葉は「どっちに近いか」です。
数直線は，数を長さに置き換えて表現している画期的な思考ツールです。
ですので，「およそ」という概念も「長さ」で表現することができ，それが，「近い」という言葉になるわけです。

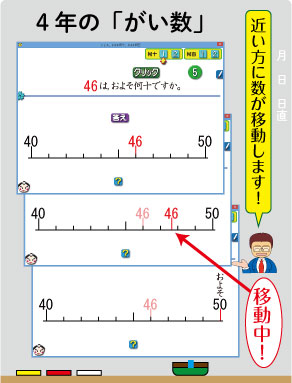
その場面のソフトが右の画像です。
『子どもが夢中で手を挙げる算数の授業』（４年５巻）に入っています。

４年の５巻には「折れ線グラフ」（ソフト数２２本）も入っていますし，「分数と分数のたし算・ひき算」（ソフト数２１本）のソフトも入っています。「がい数」の中にはソフトが１０本入っています。上の画像のソフトはその中の「０２Ａ，およそ何十，およそ何百」というソフトです。

子ども達が，４６はおよそ４０なのか，およそ５０なのか，予想をした後，いよいよ正解を見ます！
ちょっと，もったいを付けて「答え」ボタンにマウスを近づけます。グッと緊張感が高まります。
そんな中，「答え」ボタンが押されます。

なんと，４６が動き出します！
「おー！」と声を上げる子もでてきます。

５０の所に到着したら，「およそ」の文字もパッと出てきます。
画面のとおり，「４６は，およそ５０」とわかります。

何しろ，とても面白いので，もう一回やりたくなります。
３回，４回と問題を解く内に，「およそ何十か」という問題の答え方が分かってきます。数の移動がいつも近い方になっていると分かるからです。分かってくると，聞いてもいないのに，訳を言いたがる子が出てきます。授業が盛り上がっていく，面白い状況になります。

クリックボタンを何度押しても，ちょうど真ん中の一の位が５になる数は出題されません。
一の位が５になる問題は，緑色の「５」ボタンをクリックして，出題します。

「およその数というのは，近い方へ行く」と分かったら，いよいよちょうど真ん中の数での出題へと進みます。意見が真っ二つに分かれたら，かなり面白くなりますね。
これも，３回４回と見ていると，どうも繰り上がる方ばかりにいくことが理解できてきます。

概念がつかみにくい概数ですが，こうやってソフトを見ると，あっという間に理解が進みますね。

※昨年の暮れ，神戸の講演でこの場面を少し先生方にお見せしました。大きなどよめきが起こり，４年生担任中の先生が早速，『子どもが夢中で手を挙げる算数の授業』（４年５巻）を購入されていました。その先生のクラスでは，算数の時間は盛り上がっていると思います。良いですね。

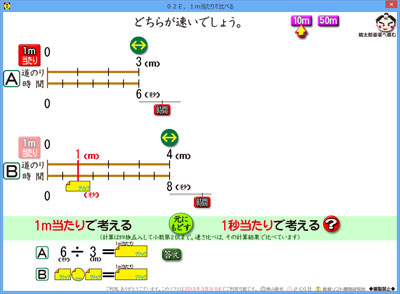６年の速さのソフトが仕上がったかのように見えたのですが，思わぬ失敗がみつかりました。

計算結果を小数第二位までの概数で求めているのですが，速さを比べるときには，どんどん割り進めた数値で比べていたのです。
そのため，答えは同じ数値になっているのに，判定ではＢの方が速いなどと食い違いが出ていました。

こういうのは，算数・数学の持つ誤差によるズレです。これもなかなか大事な応用的理解につながります。

そこの修正手間取っていましたが，何とかプログラムを直せました。
－－
ところで，上の画像のＢの線分図。これをシンプルに書くと下のようになります。

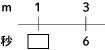
このシンプル線分図を作れるようになると，単位量あたりの問題はかなり簡単に解けるようになります。
線分図を見ながら考えれば，およそこのぐらいかなと概算できるからです。

きまりを見つけ出して，ちょっと変わった方法で解くこともできます。
線分図に，下のように田んぼの田の字のように枠を付けます。

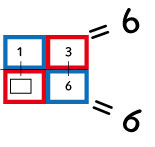
すると，斜めにかけた答えが同数になります。
赤×赤の答えと，青×青の答えが一致するのです。
なぜそうなるのかは，いうまでもありません。

この田んぼの田のような考え方は，３つの数から４つめの数を求める画期的な方法として，５，６世紀頃のインドですでに使われていました。ヨーロッパでも１６世紀頃から普及した解法です。一般に「三数法」と呼ばれています。
三数法は，小学校で習う形式で言うと，比であり，大きさの等しい分数でもあります。
かけ算関係のたいていの問題は解けるのですが，解けないタイプもあるので，そこへの注意が必要です。
そうして，中学へ行くと方程式を習い，存在感がなくなる悲しい運命を持っています。
算数の歴史的なすぐれた思考法なのですが，将来性がないのが残念なところです。

パソコンを新しくしました。
ＯＳは，Ｗｉｎｄｏｗｓ８です。

最初，ちょっと面食らいましたが，次第になれてきました。

何よりも有り難いのは，快適な仕事場になったことです。
これまで使っていたＰＣも，なかなか良い感じだったのですが，新しいＰＣは速さが違います。非常に快適です。

ディレクターもサクサクに動きますし，ソフトも立ち上がりが実に速いです。
せっかく新しいパソコンにした記念に，年末から作り進めていた６年の「速さ」のソフトの仕上げをしました。

このソフトは，かなり画期的です。
まず，「道のり」と「時間（秒）」を設定します。ＡにもＢにも設定できます。
そうして，両方の条件を見比べて，どっちが速いかを考えます。

画面に「１ｍ当たり」と「１秒当たり」が出ているので，その考え方で考えるとどうなるかを，このソフトではしっかりと見ることができます。

画面では，「１ｍ当たり」で考えるモードになっています。
Ａの方は，１ｍで考えるというのは，数直線上でどう考えることなのかが示されています。
画面のした方には，その計算がでています。

どんな感じのソフトなんだろうと思われた先生，「もっと算数」サイトにアップしますので，そちらからダウンロードしてご覧下さい。