立体の体積の学習で使える,手作り教具を御紹介します。
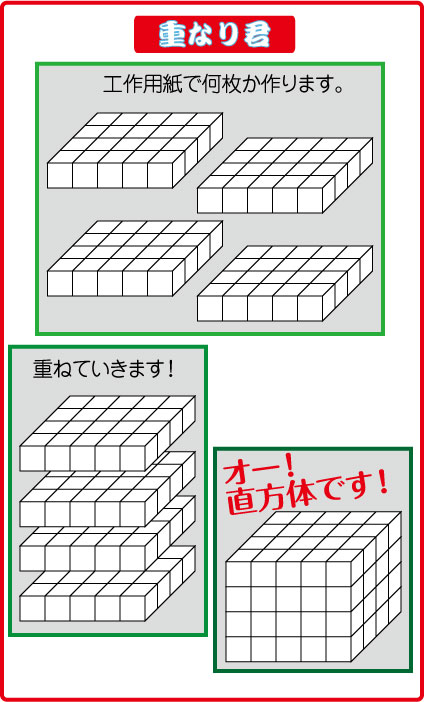
「重なり君」です。
工作用紙で積み木で1段分を作った平面図をかきます。(立体模型ではなく,単なる平面の図です)
マス目を利用すると,簡単にかけます。
それを4枚,5枚ほど作り,それぞれ切り抜きます。
そうして,下から順に重ねていくと・・・・・
なんと,直方体ができあがります。
これを授業でも使うと,「オーッ!」が出ます。
特に有り難いのは,下から積まないと組み立てられない構造になっていることです。
下から積むと言うことは,「底面積×高さ」を自然に学ぶことができるということです。ありがたいことです。
自作して,ぜひ,使ってみてください。
重ねていくだけのことですが,重ねている自分も良い気分になってきます。
また,ちょっと工夫して重ねると,面白い形ができます。実際にあれこれやってみて下さい。
この教具,よく見ると奥が少し広く見えますね。
それが気になる先生もいらっしゃると思います。その場合はマス目を利用しないで,図を描くように努力してください。
私は,プロジェクターが台形補正をするように,頭の中で認識補正をさせて授業をしていました。何の問題もありません。
ところで,立体は積むことで生成されます。
「積む」のですから,「積み初め(積む前)」 から「積み終わり(積んだ後)」までが存在しています。
その「前」から「後」までを見せるとどうなるでしょう。
中の仕組みが理解しやすくなります。
 では,「前」と「後」の間にあるのは,何でしょう。
では,「前」と「後」の間にあるのは,何でしょう。
それは,一段ずつ「重ねる」という,「動き」です。
「算数を動くようにすること」
それを子ども達に見せること。
これこそが,算数を分かりやすくする最大の工夫となります。
見れば分かる!
動けばもっと分かる!
2年生の「1万までの数」のソフトです。
数日前に,「50飛び」のメモリのソフトを御紹介しました。
「50飛び」ソフトは,すでに「もっと!算数」サイトにアップされています。
ぜひ,ご覧下さい。
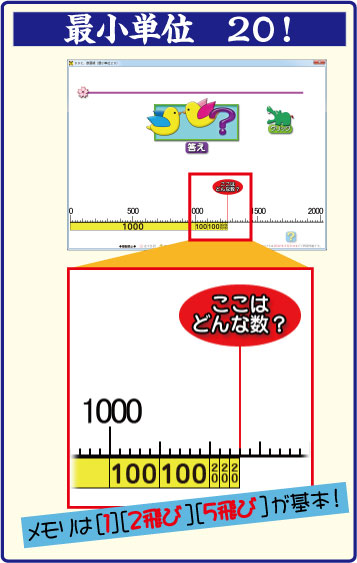
今回は,メモリが「20飛び」です。
一番小さい目盛りが20ずつになっている数直線です。
クリックとスライダーとで,何問でも問題が出題できます。
その問題に対応した,数カードが補助として表示できるように作ってあります。
どうしても,メモリが読めない!困った!という子がいたら,数カードを見せてあげましょう。
じっと見て,「アッ,そうか!」となります。
それでも,頑固に??が続いたら,数カードが見えている状態で,かつ,答えも見えている状態で,[桜]スライダーを動かしてみてください。
スライダーの動きに合わせ,数カードも増減します。答えも対応します。
きっと,わかります!
学年末,算数の復習の時間などに御活用いただけたらと思います。
--
昨日の続きで,『続・数のユーモア』を読みました。
1巻目より,続編の方が面白かったです。
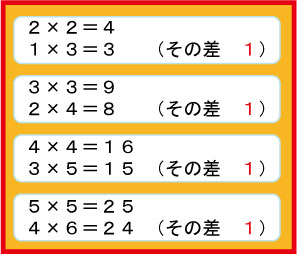 二乗のかけ算と,そこから1減,1増したかけ算の答えをよく見ると,いつもその差が1となります。
二乗のかけ算と,そこから1減,1増したかけ算の答えをよく見ると,いつもその差が1となります。
これを見ただけでも面白いです。
「不思議!」という気持ちになります。
面積の図を書いて考えると,差が1になることが,「当たり前だ!」と思えるようになります。
これだけの材料があれば,楽しく考える授業が展開できますね。
進んで考える子は,この関係からさらに発展的に取り組むこともできます。
こういう数のユーモアがたくさん収録されていました。
でも,この本は単なるパズル書ではありません。
数学的にも国語的にも,質が高いです。
表面張力を利用して,双曲線を見せる実験も載っています。
野口芳宏先生,有田和正先生が御登壇されるので,フォーラムに参加してきました。
セミナーはとても面白かったです。
名人が昔生み出した授業を,今の若い先生がICTを使って実践します。
それをVTRで見て,名人があれこれお話し下さいます。
斬新なフォーラムでした。
今回の参加者について,facebookで話題になっていました。
島根の足立先生,飯國先生,片寄先生と,愛知の古田先生とは,オフ会を!と盛り上がっていました。
その通り,オフ会が開かれ,そこには,村岡さんと,熊本の前田先生も御一緒でした。
一番不思議な感じがしたのは,足立先生,片寄先生,飯國先生,古田先生とは,この日,初めて会ったのです。
ですが,facebook上での話題が共通しているので,爆笑と共に話しが進みました。
もっとも印象的だったのは,飯國先生のジュラルミンのカバンです。
私のような年齢には,3億円事件が浮かんでしまいます。
オフ会は盛り上がり,足立先生から島根県のグループに誘われました。facebookのグループです。
なんだか,面白いなあと思いつつ,参加することにしました。
主催者の玉置先生とも久しぶりにお会いしました。
5年ほど前でしょうか。愛知のセミナーに講師として呼んでいただいた事があります。
再会できて,何よりでした。
堀田先生と初めて御挨拶をしました。
これから先,いろいろと交流が深まる予感がしています。
--
 道中,読んでいたのは『数のユーモア』。
道中,読んでいたのは『数のユーモア』。
スタートはあまり面白くありませんでした。
でも,「月のただち」と出てきたところから,急速に面白みを感じるようになりました。
「ただち」というのは,「直ち」のようで,直径という意味に読み取れます。著者の吉岡先生も「直径」と解釈していたので,なかなか良い感じに読めました。
不思議なのは,面白くないと思った本でも,途中で面白い内容が出てくると,その後は急速に楽しい気分になります。読み進めることが楽しくなってくるのです。
そうして,何とはなく,好きな本の一冊に入っていきます。
こういう,読んでいる自分の気持ちを急速に好転させる所。
そこを私は「神の舞い降りる所」と思っています。お正月で言えば,門松です。
そういう縁起の良い門松のある本でした。
この本には下巻もあるので,近日中には読んでしまおうと思っています。
--
そうそう,この本に,旧暦の1年がおよそ354日だったことが出ていました。閏月が2年半に1回ぐらい生じることになります。こういうのも面白いです。
個人的に,太陽暦に切り替わった明治5年にちょっと興味を持っています。学制が頒布された年でもあるからです。
この年は,12月2日で終わりました。でも,旧暦のままなら,その翌年には閏月がありました。
でも,翌年は太陽暦なので,閏月は消えました。
そうして,政府は12月は2日しかないのだからといって給料を支払わなかったそうです。
なんと,当時の政府は財政難だったのです。
公務員への給料支払いを減らしたかったので,太陽暦をこのタイミングで強引に入れ,12月分と,翌年の閏月分の合計2ヶ月分の給与支払いを霧のように消してしまったのです。
本を読むと,これまでの関心所とあれこれ繋がることが増えてきます。
閏月の感覚が『数のユーモア』でつかめたので,良い感じが一層高まりました。
たくさん読めば読むほど,面白くなってくるのが読書です。
「算数数学好きを増やす会」を昨年立ち上げました。
主たる活動はメーリングリスト(ML)で行っています。
会員数は10人ちょっと。ミニミニの会です。
人数はミニミニですが,パワーはかなり高いです。
このMLでは,まれに,「こんなソフトを作って欲しい」というご希望が流れます。
それを読んだ私が,「これは作れそうだな」と思えば,時間を見つけて作り,もっと算数サイトにアップします。
授業に直結した算数ソフトが,こういう所からも生まれています。
今回は,藤本先生(『わくわく☆ブラックボックス』の開発者)から,「2年生の『1万までの数』用のソフトで,最小単位が50のものと,20のものがあったら・・・」とお声を頂きました。
数直線の目盛りを読む能力は,とても大切です。
特に,「1」「2飛び」「5飛び」をしっかり理解できるように指導することが大切です。
その指導が,3年生の棒グラフ,4年生の折れ線グラフ等で底力として有効に働くからです。
そんな思いが頭を駆けめぐり,1本作ってみることにしました。
製品版の『1万までの数』には,最小単位が100の数直線ソフトが収録されています。
これでも十分によい勉強ができます。
その数直線ソフトのプログラムを活用して,最小単位を50まで学べるソフトを開発中です。
間に1目盛り増えると,メモリが混雑します。そこで,全体を5000までとして,メモリの間隔が狭くなりすぎないように配慮しました。
見所は,数直線の下に「1000」「100」「50」のカードが並ぶことです。
これが3750の「量感」と「数の構成」を視覚的に伝えています。
算数がイマイチと思っている子には,こういう仕組みの見える教材を見せることが肝要です。
次第に算数の理解が進むからです。理解できれば,算数は面白い勉強になります!
日曜までには,もっと算数にアップできると思います。
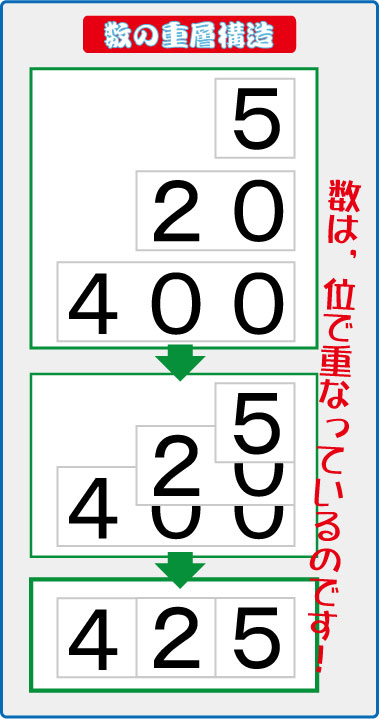
「数の重層構造」と呼ばれる,数の学習用教材です。
考え方は,とても簡単です。
-----
◆ 2桁以上の数は,位毎に階層を作っている
-----
と考えます。
この考えに従って,階層毎のカードを作ります。
これで準備はOKです。
授業では,カードを重ねて用意しておきます。
子ども達にカードを見せ,「読みましょう!」などと,勉強を始めます。
「425!」と元気に答えてくれたら,簡単に問題を出します。
「425って,何と何と何でできている数ですか」
ピンと来ない子がいても,いっこうにかまいません。
重ねた紙をばらせば,誰でもすぐに分かることだからです。
「見れば分かる」というのは,とても重要な学習法です。
目と耳とでは情報の処理能力に大きな違いがあるからです。
 その差は,何と500倍以上。
その差は,何と500倍以上。
目から入る情報は,耳からはいる情報より圧倒的に多く処理されるのです。
ですから,数の重層構造を,
「いいですか。425というのはね,400と20と5からできているんだよ」と,声で説明をしても,子ども達の頭が処理する情報は,カードを見たときより,うんと少ないのです。
◆ 陰に隠れている「0」の情報も入りません。
◆ 重なる過程で見る形成の様子も情報として処理されません。
教材を準備して授業をすることが,いかに大切なことなのか,こういった処理量からもわかります。
--
 「数の重層構造」の考え方は,算数ソフト(2年3巻)にも生かされています。
「数の重層構造」の考え方は,算数ソフト(2年3巻)にも生かされています。
[クリック]ボタンをクリックすると,次から次へと数が変わります。
数をマウスでドラッグすると,右のようにカードをバラせます。
[整列]ボタンを押すと,数カードがきちんと重なり,普通の数の状態になります。
数カード教材や算数ソフトを使って,算数を視覚的に示すように心がけましょう。
子ども達は,見ることで算数的体験をし,算数の豊かさを吸収していきます。
新作を1つ作りました。
1年生の「100までの数」で使える算数ソフトです。
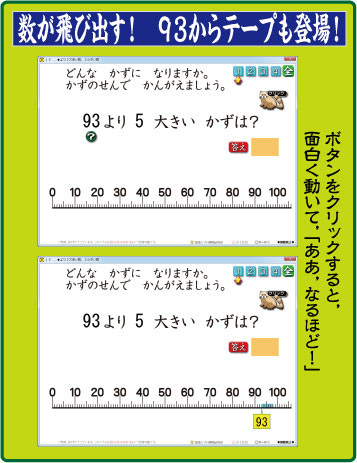
クリックすると,問題が登場します。
「93より 5大きい数は?」
「45より 3小さい数は?」
こういった問題が,ジャンジャカ登場します。
気を配ったのは,数直線です。
基準となっている元の数から,「大きい場合は右へ」。
「小さい場合は左へ」とテープが伸びるようにプログラムしました。
左右どっちにテープが伸びるか。
これがなかなか重要なところなのです。
通常の感覚では,「大きい」と記されると,図体が大きいとなります。
「5大きい」と言われれば,元の状態より5だけ見た目が大きくなるのが,通常の感覚です。
でも,算数にはこういう日常的な感覚を受け入れない世界があります。
数直線は,まさにその世界です。
数直線は左に小さい数,右に大きい数を表す約束になっています。
ですから,右に行けば行くほど大きく,左に寄ればどんどん小さくなります。
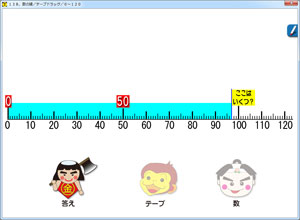 その理解ために,93というのは,「0から93までの長さ(量)」を表していることを理解しておく必要があります。
その理解ために,93というのは,「0から93までの長さ(量)」を表していることを理解しておく必要があります。
それを『子どもが夢中で手を挙げる算数の授業』(1年2巻)に収録されている「100までの数」ソフトで十分に理解していることを前提に,このソフトが作られています。
元の数から見て,「5大きい数」というのは,元の数から右に5めもり分移動した位置。
元の数から見て,「3小さい数」というのは,元の数から左に3めもり分移動した位置。
数直線上での「大きい」「小さい」の感覚を学べるようにと作り込んだのがこのソフトです。
中学で「93+(+5)」や「45+(-3)」といった数の計算を学ぶときも数直線で思考します。
学年はかけ離れていますが,考え方は通じています。
数学に通じる学習を,1年生から視覚的にしっかり学べるのです。
大きな力が付きます。
有り難いです。
近日中に,もっと算数サイトにアップします。
御活用ください。


![キーワードでひく小学校通知表所見辞典[増補版] -2057文例◎ぱっと開いてすぐ書ける- CD-ROM付](http://www.kennya.jp/app-def/S-102/kennya/wp-content/uploads/2014/08/76-8.png)















