『遠山啓』は面白いですよ。
今日も一つ、グッと来たところを引用しましょう。
エンゲルスは弁証法の主法則として、“量と質との転化” “対立物の相互浸透” “否定の否定”という三つの法則を上げている。（ｐ１７７）
頭の良い子はなぜすぐに分かり、そうでない子はなかなか分からないのか。
若い頃から、この極めて自然に現れてくる現象の原理がどうなっているのか、どう理屈づければ、この問いへの解答となるのか、と考えることがありました。
この疑問は、引用した「量と質の転化」の問題となって私の課題となっていました。
量をこなすことで、質的に変化していく。
その構造はいかなる様相をしているのか。
その答えとなりそうなことが、前回も引用したところに記されています。
それは質の差ではなく量の差に過ぎない（ｐ２４１）
優れた見識です。
子どもの頭に質的な差があるのではなく、こなした量に差があるのだと言うことです。
量をこなせば、誰でも分かる！
遠山のこの言葉は、そういう命題を示しています。
これは、教師をやっていればそう願わずには居られません。
たくさん練習してできるようになる子。
少ない練習でできるようになる子。
そこにあるのは、量的な差だけと考えたいのが教師なのです。
と思っても、その差が大きくなってしまうと、心がくじけます。
どうにも質に差があるように思えてきます。
恐いのは、この瞬間です。
質に差があると見なしてしまうと、それはもうお手上げという感覚に襲われ、教育の無力さが頭を覆い始めます。
こういう落とし穴的思考にフタをして、「量の差とは何なのか」という問題意識を持っていると、出会うべき本に出会うようになります。
私の場合はデカルトの『精神指導の規則』でした。
尚それらすべを記憶して居らねばならないのである。この故に私は、一々を直感すると同時に他に移り行く一種の連続的な想像の運動によって、幾度もそれらを通覧するであろう。（ｐ３１、岩波文庫）
一つの事例を見ることで、その事例で何が起こったかが頭の中に入り、それを忘れない内に次の事例、さらに３つ目の事例をみること。
これができるのが頭のよい子で、２つ目、３つ目の事例に接する頃には１つ目の記憶が消えかけてしまうのが、そうでない子の頭の働きなのです。
よく、１時間で１問の問題を考えるタイプの授業があります。
これは、翌日まで、記憶の持続を求める学習になるので、そうでない子がアウトになるようにしむけている授業とも言えます。
大事なポイントは、忘れない内に次の事例を示ていく活動をすることです。
「短時間」がキーワードになります。
こういう思いがあって、算数ソフトをつくりました。
ですので、私の作った算数ソフトは、その大方が理解の伴う類題を連続的に出題できる仕組みにしています。
短時間の内に類題を数問体験することこそが、遠山啓の言う「量の差」を克服する方法なのです。
このあたりのことを、御存命だったらお話ししてみたかったですね。
算数ソフトも見てもらいたかったですね。
－－
関連記事：
「小学生のころ、最も印象的な国語の話は、『雨の早慶戦』です。」
と、何かの拍子に話したことがあります。
隅田川あたりで行われたボートレースの話です。
私は「雨の早慶戦」という題だったと思っていたのですが、ネットで検索をしたら、違っていました。
「あらしのボートレース」でした。
改めて、この話の全文を読んだのですが、小学生の時のわくわく感同様に、強い感動を受けました。
嵐ですので、ボートに雨がたまります。
川と言えども波が立つので、川の水もボートに入ってきます。
慶応ボート部は最後まで全力でこぎ続ける道を選びました。
早稲田ボート部は半数の４人が桶で水をかい出し、残った４人がこぎ続ける道を選びました。
はじめ慶応が大きくリードしていましたが、次第にボートに水がたまり速力が落ちます。
そうして、ゴール手前でついに沈んでしまい、早稲田の勝利となります。
この話は非常に教訓的に私の中に残りました。
がむしゃらに進むんじゃない！
状況を考えて、それなりの準備をしろ！
この年になって読み返してみても、同様のことを感じます。
歳をとったせいか、大会委員長は延期の判断ができなければ・・・とも思いました。
この感動的な、道徳的な話。
なんで国語の教科書に載っていたのでしょう。
ふと思ったら、当時はまだ道徳の副読本すら無かった時代と思います。
それでも、道徳は教えなければと考えて、国語の中に道徳教材をまぶしていたのではないか。そんな気がしています。
では、この「あらしのボートレース」を、国語らしく、早稲田の選手はどんな気持ちだったでしょうか。慶応の選手はどんな気持ちだったでしょうかと問うたら、どうでしょう。
せっかくの教訓的な内容がかすれてしまいます。
心情曲線を書いたらどうなるでしょう。教訓的な世界からどんどん離れます。
ましてや、どこから見ているでしょうかと視点を気にしたら、道徳からは絶望的な状態となります。
教訓的な力のある教材は、国語のように迫らない方が良いのです。
では、どう授業を進めたらいいのか。
それには、「自然道徳」と「学問道徳」を念頭に入れるところから考えることになります。
すると、「困難」の構造を把握する授業になっていくでしょうね。
道徳は、やっぱり論語を読むことです。
私の机の上にも、『日めくり論語』があります。
毎日見ているだけも、良い勉強になります。
－－
関連記事：
英語のわくわくプリントの新作が、さくら社ＨＰにアップされました。
関心のある先生、ぜひ、御活用下さい！
＜こちら＞です。
今日は、読書ぐらいしかできないまとまった時間があったので、『遠山啓』を読みました。
これは、名著ですね。
よくぞ、ここまで編んで下さったと、ありがたい気持ちで一杯になります。
いつもなら、ペンでガンガンに印を付けるのですが、畏れ多い気持ちが湧いてきて、薄く少し書くにとどめました。
それでいて、勇気が湧いてくる、実に素晴らしい本です！！
◎ 身近なものほど“経験しやすい”ことは事実だが、“認識しやすい”とはいえない。（ｐ２１４）
◎障害児を「特殊」とみなす教育観から脱却し、それは質の差ではなく量の差にすぎないという人間観・知能観に立ち、人間としての知的発達をあきらめず、指導のしかたを工夫しさえすれば、健常児同様、障害児も抽象的な概念に接近していけるという事実を見せられ、滝沢は驚愕したことを率直に告白している。（ｐ243-244）
５０年も６０年も前、まだコンピュータが身近になかった時代に、遠山啓はここまで見通していました。
私も量をこなせば質に転化することは、「量質転化の法則」から、実にそうだと信じていました。
しかし、実際にそれを算数の授業で展開することは、できませんでした。
繰り返しの授業をしても、肌感覚で質的に転化することを実感できなかったのです。
肝となる「短時間」「大量の反復」の両方を満たすことが、黒板の授業ではできなかったのです。
時は流れ、ＰＣが登場。
ソフトを使って授業ができるようになりました。
「量質転化は起こる！」と確信していたことが、現実となりました。
それが、日本のみならず、ルワンダでも。
◎障害児に「２＋３」を教えるとき、実物のタイルを使って説明しても、２のタイルと３のタイルは離れたままで、「足して５」というまとまりになることを理解できなかった。だが、二つのタイルをぶつけてカチンと音をたてるようにしたら、はじめてひとつになったことを理解してくれた。（p251）
ここを読んだ時、算数ソフトを遠山先生に見ていただきたかったと痛烈に思いました。
動きを見せること。
それを短時間に繰り返し見せること。
効果音を入れること。
これこそが理解への究極の道なのです。
この本を読んでいると、遠山先生が算数ソフトへ太鼓判を押して下さっている気持ちになります。
そうして、「横山先生、やれることを精力的にやり進めてください。」と声をかけられている気になりました。
夢に描くアフリカプロジェクト。
アフリカチームの皆さんと一緒に、しっかりと進めたいと思います。
この本、読むのは４時間ほどでした。
しかし、この本は制作に時間がかかっただろうなと思います。
数年、いや５，６年はかかったのではないかと、読書中に思いました。
奥付には、「本書の執筆と制作にほぼ二年を要しました。」とあります。
にわかには、信じがたいです。
資料の整理がそうとうできている状態ということが推察されます。
この仕事をされた著者の友兼清治氏の情熱、勉強になります。
－－
関連記事：
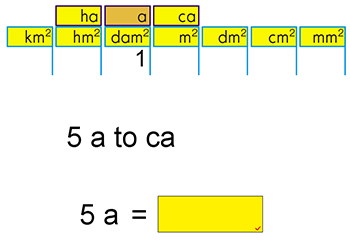
小数の数直線ですが、小学校の先生は、これにも違和感を感じるでしょうね。
「１．０はダメだろう！ ここはやっぱり、１だよ。」
てなことがフッと浮かんできます。
初めて小数を学ぶとき、「１」と「１．０」はどっちの方が理解しやすいのでしょう。
そんなことを考えると、次第に１．０に軍配を上げたくなってきます。
なぜなら、「１の位が１」で「小数第１位が０」という位取りの思考が、パッと見た、見た目で伝わってくるからです。
それを便宜的に「１」と書いていると扱った方が、筋が良いと感じます。
また、ちょっと見方を変えると、１年生で習った「１ ２ ３ ４ ５ ６ ７ ８ ９ １０ １１」の表し方にも近いと感じます。
とは言っても、１とか２とか３とか、すでに知っている数があります。
そこに小数を学ぶのですから、整数の間に小数が存在していると考えることもできます。
すると、「１．０」ではなく、「１」の方がすっきりします。
前者は数として小数があり、その一部が整数と把握させるタイプですね。
後者は生活に基づいて、整数の間に小数は存在すると、とりあえずみていくタイプです。
どちらにしろ、時間と共に、両方の感覚がわかるようになるので、大きな問題にはなりません。
大事なことは、柔軟に把握することです。
－－
関連記事：
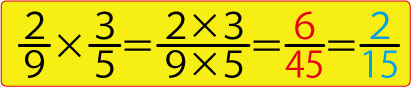小学校で習う分数のかけ算です。
この計算に取り組んだのですが、この取り組みを見て、「ムムッ！」と感じるものがある人は、きっと小学校の先生ですね。
このやり方をすると、バツになる可能性もあります。
それは、途中で約分をするのが一つのきまりのようになっているからです。
所変わって、ルワンダ。
こちらでは、図のように計算をしています。
かけ算ですから、まずはかけ算をキチッと実行。
しかる後に、必要があれば約分をする、と行っています。
日本のように要領よく計算すると言うよりは、キチッと順序通りに進める感じがします。
この方法の良さは、赤いところまでにややこしい約分がないことです。
赤の所は既約分数にこそなっていませんが、正解の範囲です。
何というか、ここにちょっとした人生訓を感じます。
「まずは正解の射程範囲に入ろう！」
そういう正解エリアにいち早くインすることこそが、最も大事なことなのです。
より分かりやすい既約分数にするかどうかは、あとからゆっくり調整すればいいのです。
言うなれば、約分は誤差の範囲となります。
ところで、こういう分数の計算をプログラムする時、一番難しいところはどこだか、わかりますか。
最大公約数をプログラムで抽出する所です。
「３と９」の段階で見つけるにしろ、「６と４５」の段階で見つけるにしろ、頭の中には「３だ！」と最大公約数がすぐに出てきますが、その「３」をどうやって浮かび上がらせたかのか。それを論理的に書き表す作業がプログラムなのです。
しかも、２つの数が「２５と１５」と変わっても、変わることのない計算式を考え出します。
へこたれそうなほど、頭を使います。
でも、一度、うまいこと計算式を見出すと、不思議と次の時は悩みが少なくなり、上達を感じます。
プログラムは論理的思考を鍛えられるのですが、どう考えたら良いかという「発想」が先に立ちます。
その「発想」の下、論理的に一つ一つ組み立てていきます。
プログラミングは論理能力も鍛えられますが、それ以上に発想力が鍛えられるありがたい世界でもあります。
算数ソフトは面白いですね。授業でドンドン使って下さい。
新しい時代の学習は使っている先生の教室から生まれてきます。
－－
関連記事：
６月２５日（日）は大阪で野口塾です。
前日の夕方に大阪入りをします。
どうも、前夜祭が開催されるとのことなので、ちょっと顔を出そうかと思います。
前夜祭には野口先生、中嶋先生に加え、事務局の阿部先生達が参加します。
楽しい一時になりますね。
今日は、『遠山啓』が届きました。
こういう本が出ていることを、ＳＧ会の竹尾さんから教えていただきました。
水道方式を読み返していたところだったので、何というタイミングでしょう。
この本は分厚いです。
「分厚い本は、難しい本。」
これが私の中に形成されている一つの本スタイルです。
なので、ちょっとまずかったかなと思いました。
少し読んでみると、読みやすいことがわかったので、今夜あたりから読んでいこうと思います。
遠山啓というと、私には学生時代から新卒時代が思い出されてしまいます。
南郷継正の武道論や、三浦つとむの言語論などと共に、熱中して読んでいました。
あの頃の本を、今一度、「弁証法と創造」という観点から読み返したいと思っているのですが、他にもやりたいことがあれこれ出てきてしまい、ずるずるとしています。
でも、この本の遠山先生を見て、早い内にそういう勉強をすませておこうと思いました。
－－
関連記事：
