昔の算数の教科書を見たことがありますか。
アッと驚くほど，数・数・数・・・のオンパレードなのです。
今の時代の教科書を知っている先生方には，すぐさま「これじゃあ，分からない子がたくさん出るだろうな」と感じると思います。
「わかりやすさ」という視点で，ザラッと算数の教科書を昔から見ていくと，なんとはなく４つの段階になっているように見えてきます。
第１段階は，「数」の時代です。
数や計算一色という感じの時代です。
それが，次第に挿絵が増えてきます。太平洋戦争中の１年生の教科書は，ほぼ全部絵で，逆になんだか？？という気にもなるぐらいです。これが第２段階です。
第３段階は，数直線・線分図の登場です。戦前から数直線は教育書などには出てきていますが，教科書はちょっとひ弱でした。それが，戦後，随所に出てくるようになっています。
数直線は，「数」と「量」を同時に示している「数量」の表現です。デカルトの発明で，非常に優れた表現です。
そうして，最近，教科書の巻末に手作り教具がおまけとしてついて来ています。
この手作り教具は，「数」「量」「数量」とは全く異質の表現を含んでいます。それが「動き」です。
教科書には取り入れられていませんが，「動き」を実に巧みに実現させているものがあります。
皆さんが使ってくださっている「算数ソフト」です。これが，第４段階です。
算数の勉強をしている先生は，「数」「量」「数量」については目にしているので，それほどの違和感がないと思いますが，「動き」は算数としてあまり聴かないので，「どうなの？」と感じると思います。
「動きは算数じゃないよ！」そう思う先生もいると思います。
でも，「動き」は，算数の本質的な部分なのです。
「数」「量」「数量」は，算数の「結果」を示した表現です。
それに対して，「動き」は算数の「過程」を示しているのです。
このように一言で言われても，わかりにくいだろうと思いますが，その「過程」は「連続」という姿を持って表れ，どうも５種類あると私は見ています。
この「動き」の表現，特に算数ソフトによる動きの表現は，子ども達の理解・定着を著しく上昇させています。
第１段階から第２段階へ発展したときより，
第２段階から第３段階へ発展したときより，
はるかに大きなわかりやすさを子ども達に与えています。
新しい衝撃的な研究領域。それが算数の「動き」です。
昨日届いた本です。
１６０３年につくられた，日本語をポルトガル（葡萄牙）語に直す辞書です。「にっぽじしょ」とよみます。
この本は，その日本語版です。こういう本を作ってくれた岩波書店に感謝です。
なにしろ，この本は徳川幕府が開かれた頃の日本語ドドーンと載っている非常に貴重な資料なのです。
日本にとっても貴重ですが，ポルトガルにとっても貴重です。当時のポルトガル語がこの本に残っているからです。
この辞書はＡＢＣ順になっているので，検索が大変です。ですので，調べるために使うには，その準備が必要となります。それには，まず，読む事です。見出し語をザラッと。
そう思いつつ，昨日は，パラッと開きました。
「地検」が載っていました。土地を測量することです。
「検地」もあるかなと思って調べたら，これが分からず，今日まで持ち越しました。ようやくさっき見つけました。「Ｑｅｎｃｈｉ」です。まさか，Ｑで来るとは思っていなかったので，ちょっと時間がかかりました。
でも，これで「Ｑｅ」のところに「け」と付箋を貼れば，この先が楽になります。
そうそう，昨日は， 「Ｃｏｃｏ」（九九）を見つけて，感動しました。「計算表」と載っていました。
国語辞典に飽き足りなくなったら，こういうハイクラスの辞書も良いですよ。
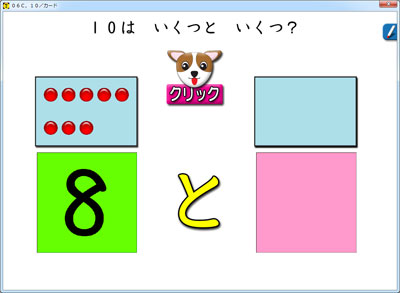
「１０は２と？」
こんなの簡単！と思われるところですが，なかなかサッと答えられない子がいます。
数を「数える」ことに慣れ親しんでいるので，２つに分けたり，組み合わせたりすることには，とまどいを感じるのです。
それなので，おはじきやブロックなどを使って， 「１０は４となんだ」など，具体物を見ながら勉強をくり返します。
それでも，イマイチの子がでてきます。
数えられるならそれでいいよねと，軽めに扱って次へ進んしまうことも起こりえます。でも，これはなりません。１０の合成分解の考え方が，繰り上がりのあるたし算の途中に，中継する思考としてしっかり位置付いているからです。
ですので，この勉強は教科書の該当ページが終了しても，折を見て繰り返ししっかりと定着させていくようにします。
１年生の教室に算数ソフトをもって授業に入った山本先生。
そうです。あの『伝わる伝わる見える指導』の山本正実先生です。
奇跡の算数ソフトをＰＣにセットして映し出し，リズム良く，繰り返し３０問ほどやったそうです。（５分もかかっていません）
１年生なのですが，すでに勉強時間に「ウップー」とうつぶせ気味になる子もいます。
そんな子も，みんなどんどん答えて，最後には全員の子がすっかり分かるようになったそうです。
ご覧の画面のように，犬をクリックすると，「８」が他の数に早変わりします。
答えは，水色とピンクの四角をクリックすれば，直ぐに見る事ができます。
効果音も適度に鳴って，雰囲気を盛り上げてくれます。
くどくど説明するより，どうなるかを繰り返し見る事が大切です。繰り返し見る内に，そこに横たわるきまりに子供自身が気付くからです。
自分できまりに気付くから，とっても面白く感じるのであり，また，忘れにくいのです。
『子どもが夢中で手を挙げる算数の授業』１年１巻です！
算数ソフトを使わずに授業を進める事は，見方を変えると，わかりにくい授業をしている事になります。
奇跡の算数ソフトをじゃんじゃん使いましょう！子ども達の学力増進のために！
算数の九九。昔は九九八十一から始まっていたのですが，どうも，戦国時代あたりから「二二が四」と小さい方から一覧されるように変わったようなのです。
この変化の原因が中国大陸にあるような気がして，その移り変わったのではないかと思われる時代の大陸を覗いてみたくなりました。
あれこれ調べて，まずは，右の『大モンゴルの世界』から読む事にしました。
読み終えて，この本からは調べたい事については，その輪郭を知ることができ，ちょっと前進！という思いです。
でも，それ以上に，ビックリする事を学びました。
蒙古来襲とか元寇とか，「一方的に攻めてこられた」という意識で学んできたので，元は好戦的な国と勝手な思いこみができていました。それが，この本を読むと，一変します。
２回目の元寇では，大量の船が１ヶ月も海上に停泊していました。どうも，これは戦いの船ではなく，農耕移民だったようなのです。
そんな事，突然，ここに書かれても，何が何だか？？と思います。
４章の中程に日本との事がしっかりと書かれています。そこだけでも，目を通していただくと，広い視野に立ったモンゴルの姿が分かります。
また，その後には，「周礼」が出てきます。
大都（今の北京）建設は，「周礼」に出てくる「古代中国の国都の理想型を忠実になぞったかたち」になっているのだそうです。これも，驚く事です。民族が違う文化の，それも古典様式に則って首都をつくったのです。気配りとか配慮とか言う感覚ではなく，これが生き方だったのだと思い知らされます。
モンゴルへの意識がどんどん変わっていきました。
そうして，次の１文を読み，大きく考えさせられました。
「世界史の大流をふりかえると，民族や人種・宗教・文化伝統などがぬきさしならぬ対立要因となるのは，むしろヨーロッパ流の国家・民族・宗教の観念が世界に広まりだした十九世紀以降に顕著になったものではなかろうか。」
とても良い本です。お勧めします。
気になる本をヤフーオークションで見つけると，ちょっと先の事を考えて，入札する事があります。昨日と今日と，珍しく２日連続で入札し，落札しました。
１つは，『日葡辞書』です。国語辞典で満足できなくなってきた国語系の先生が，食指を伸ばしたくなるのがこの辞書です。私自身，長い間気になっていて，ちょっとあれこれ考えて，購入する事にしました。オークションでしたので，古本屋価格の半額で買えました。良かったです。
もう一つは，『初等数学史』です。 算数ソフトの開発を進めていると，どうしても「どう教えるか」という一点に集中します。年がら年中，この頭だと，見ているはずの算数が次第に見えなくなってきます。近視眼になっていく感じになります。そうなり過ぎないように，昔の事を学ぶようにしています。
今，ちょっと気になっているのが，この『関大初等部式 思考力育成法』です。半年前に出た本なので，すでに読み終わっていますが，どうも，気になります。
たくさんの思考法（スキル）を教科毎に束ね，さらに全教科対応へと束ね，最終的に６つのスキルに集約させています。この流れが，算数・数学の「記号化」に近い感じなのです。
記号化というのは，「合わせる」とか「ふえる」とか「加える」などいろいろな表現を「＋」に束ねていくような作業です。
束ねてしまうので，記号化は何とはなく視野を狭くするような感触も受けます。
しかし，算数の世界で見ると，狭くなるどころか，視野はどんどん広がります。記号を知った子は，反復練習によって，その記号を使って習った事象以外の事象へも自然と適用を行い始めます。花壇の花の数から「＋」を習った子が，人の数で「＋」を練習し，消しゴムの数でも「＋」を練習し，どんどん練習しているうちに，自然と，その他の諸事象に「＋」を適用するようになるのです。
算数の記号は「＋」だけではありません。「－」も学びます。「×」も「÷」も学びます。すると，それを組み合わせて思考する力が出てきます。
ここまで考えただけでも，『関大初等部式 思考力育成法』には，武者震いのような感触がしてきます。何か，これまでにない思考の世界を開きそうだと感じてくるのです。
この本の著者の一人である三宅先生のお話を一度伺ってみたいですね。私はただひたすら，「記号化」と「適用」という意識で聴いていたいです。
この本は良い本です。お勧めします。
指を使って計算する事が，ちょっと話題になりました。
これは，昔から賛否両論ありますが，意見をお持ちの方は，たいていどちらかが良く，どちらかが悪いと考えています。
私は小学生の頃，算数が得意でした。でも，計算をするときは，暗算だけに頼らず，ちょっとでも不安に思うときは，必ず指でこっそりと確認をしていました。答えが確実に正しくなるように子供心に最善策を講じていたのです。
こういう経験があるので，指を使う子には，そのまま指を使いなさいと話していました。
前の学年で使ってはいけないとしっかり指導を受けていた子は，かなりビックリした顔になります。
小学校で教えている計算は十進位取りによる計算なので，筆算の形で学ぶのがベストです。
右側から一の位，十の位，百の位と配置され，わり算以外は小さな位から進めます。
指で数えるのは，こういった位取り計算法とはちょっと違う世界観になりす。
どちらかというと，指は「そろばんタイプ」なのです。一桁ソロバンという感じです。
珠の変わりに指を折ったり伸ばしたり。
２と言われて，２本まとめてバシッと伸ばすのは，さながらソロバンで一珠を２つまとめて動かすのに似ています。
私がすごいなあと思うのは，４と言われたときに，４本伸ばすというより，１本（親指）だけを曲げるという補数で指の動きを表現することです。これには，時々，「かなりお利口！」と思う事があります。
その指折り数えるという方法ですが，古くは万葉集に出てきます。山上憶良の歌です。
秋の野に 咲きたる花を 指折りて かき数ふれば 七種の花
指を折って数えてみたら・・・と歌われています。奈良時代には確実に十進法が文化として定着していた事が分かります。
そうはいっても，やっぱり指は・・・と思う方もおられると思います。
指の難点は，引き算に弱い事です。逆に数え，指も逆に動かすのはなかなか難しいです。そういう障害があるので，指を使う子は，引き算を引く数から順に数える方法でかわしていきます。このあたりになると，指はちょっと・・と感じてきます。
教科書に出てくる十進位取りの考え方は，１０の束を考える計算方法です。
これの良さは，慣れるとパッとわかる点にあります。
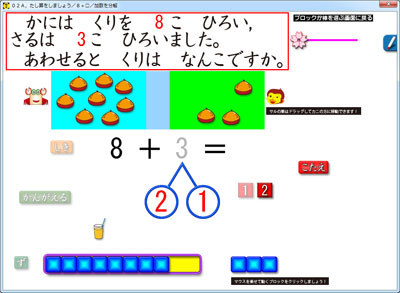
教科書には，ソフト画面のようなサクランボの形がでてきます。計算の仕組みを理解させるアイデアです。８は後２で１０だから，３を２と１に分けて，８と２で１０にして・・・と考え進めます。
また，教科書にはブロックか棒がでてきます。具体的に栗で考えると「１０の束」が明瞭にならないので，ブロックや棒で思考を助けています。 算数セットなどに入っている，算数的思考の必須アイテムです。
大事な一点は，この１０の束をつくる様子を何度も見る事です。
ここが手作業になるので，なかなか見せづらく，理解がイマイチのまま計算に入り，気がつくと指でやってしまうのです。ソフトで何度もみて，感覚を養う事が肝要です。そうして，指は押さえで使うぐらいになればグッドです。
