中国思想を読んでいる内に，いつかきっと，買うことになるだろうと思っていた本を買いました。
『中国古典名言辞典』です。
なかなか購入できなかったのは，この本の作りに敷居の高さを感じていたからです。
第１章が論語，２章が孟子，３章が大学・・・とこういう順に名言が掲載されています。
開いてみたとき，「これでは・・・」と残念に思った事があります。
それが今では，なんだかこの作りが良い感じなのです。
今の感触で古典を読んだら，後にはかなり有益な本になると感じ，購入に至りました。
先ほども「荀子」の「宥坐」の所を読みました。
手元の『荀子』の該当箇所と微妙に書き方が違っています。
おかげで，良い言葉に触れることができました。
「満則覆」 満つれば即ち覆る
「宥坐之器」が登場するお話しです。
「得意になりおごる者は，必ず滅びる」と締めくくっています。
グッと良い気持ちになります。
中国古典に限らず，古典を学ぶことは，「良い言葉体験」なのだと思っています。
日頃，世俗的な言葉にずっぽりと使って生活をしているので，時々，古き良き言葉に触れて，そこから人としての道を迷わないように・・・などと思うのです。
「算数数学好きを増やす会」を昨年立ち上げました。
主たる活動はメーリングリスト（ＭＬ）で行っています。
会員数は１０人ちょっと。ミニミニの会です。
人数はミニミニですが，パワーはかなり高いです。
このＭＬでは，まれに，「こんなソフトを作って欲しい」というご希望が流れます。
それを読んだ私が，「これは作れそうだな」と思えば，時間を見つけて作り，もっと算数サイトにアップします。
授業に直結した算数ソフトが，こういう所からも生まれています。
今回は，藤本先生（『わくわく☆ブラックボックス』の開発者）から，「２年生の『１万までの数』用のソフトで，最小単位が５０のものと，２０のものがあったら・・・」とお声を頂きました。
数直線の目盛りを読む能力は，とても大切です。
特に，「１」「２飛び」「５飛び」をしっかり理解できるように指導することが大切です。
その指導が，３年生の棒グラフ，４年生の折れ線グラフ等で底力として有効に働くからです。
そんな思いが頭を駆けめぐり，１本作ってみることにしました。
製品版の『１万までの数』には，最小単位が１００の数直線ソフトが収録されています。
これでも十分によい勉強ができます。
その数直線ソフトのプログラムを活用して，最小単位を５０まで学べるソフトを開発中です。
間に１目盛り増えると，メモリが混雑します。そこで，全体を５０００までとして，メモリの間隔が狭くなりすぎないように配慮しました。
見所は，数直線の下に「１０００」「１００」「５０」のカードが並ぶことです。
これが３７５０の「量感」と「数の構成」を視覚的に伝えています。
算数がイマイチと思っている子には，こういう仕組みの見える教材を見せることが肝要です。
次第に算数の理解が進むからです。理解できれば，算数は面白い勉強になります！
日曜までには，もっと算数にアップできると思います。
手作りの算数教具を，一つ御紹介しましょう。
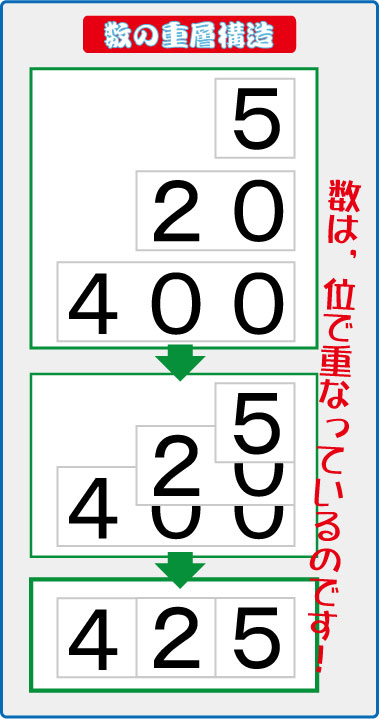
「数の重層構造」と呼ばれる，数の学習用教材です。
考え方は，とても簡単です。
－－－－－
◆ ２桁以上の数は，位毎に階層を作っている
－－－－－
と考えます。
この考えに従って，階層毎のカードを作ります。
これで準備はＯＫです。
授業では，カードを重ねて用意しておきます。
子ども達にカードを見せ，「読みましょう！」などと，勉強を始めます。
「４２５！」と元気に答えてくれたら，簡単に問題を出します。
「４２５って，何と何と何でできている数ですか」
ピンと来ない子がいても，いっこうにかまいません。
重ねた紙をばらせば，誰でもすぐに分かることだからです。
「見れば分かる」というのは，とても重要な学習法です。
目と耳とでは情報の処理能力に大きな違いがあるからです。
その差は，何と５００倍以上。
目から入る情報は，耳からはいる情報より圧倒的に多く処理されるのです。
ですから，数の重層構造を，
「いいですか。４２５というのはね，４００と２０と５からできているんだよ」と，声で説明をしても，子ども達の頭が処理する情報は，カードを見たときより，うんと少ないのです。
◆ 陰に隠れている「０」の情報も入りません。
◆ 重なる過程で見る形成の様子も情報として処理されません。
教材を準備して授業をすることが，いかに大切なことなのか，こういった処理量からもわかります。
－－
「数の重層構造」の考え方は，算数ソフト（２年３巻）にも生かされています。
[クリック]ボタンをクリックすると，次から次へと数が変わります。
数をマウスでドラッグすると，右のようにカードをバラせます。
[整列]ボタンを押すと，数カードがきちんと重なり，普通の数の状態になります。
数カード教材や算数ソフトを使って，算数を視覚的に示すように心がけましょう。
子ども達は，見ることで算数的体験をし，算数の豊かさを吸収していきます。
尊敬する坪田耕三先生の『算数のなぞ』です。
表紙を見ると，子ども向けの本だなと思い，教師としては購入をためらいたくなります。
しかし，この本はお薦めします。
なにしろ，算数の奥深いところがしっかり記されています。
その上，簡潔に書いてあるので，実にわかりやすいです。
◆３年生，４年生の学年末といえば，「そろばん」でした。
かけ算九九で「ニニンがシ」「シイチがシ」と「が」がつくのは，このそろばんと関係しています。
◆分数の横棒の名前，坪田先生に教わりましたが，それも載っています。
◆計算の「アルゴリズム」が人名が由来であることも載っています。
教科書に書いてある内容をきちんと指導することは必須のことです。
ですが，そこにちょっとした算数的教養をまぶせると，算数の質がグッと高まります。
この本にはそういう材料がたくさん載っています。
感動的なのは「おでんのマーク」です。
かけ算で数を表すとどうなるか。
なんと，素数と合成数が楽しく学べるのです。
それを表にすると・・・・。
坪田先生の算数は最高です。
新作を１つ作りました。
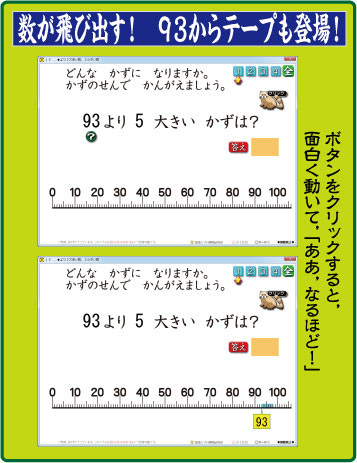
１年生の「１００までの数」で使える算数ソフトです。
クリックすると，問題が登場します。
「９３より ５大きい数は？」
「４５より ３小さい数は？」
こういった問題が，ジャンジャカ登場します。
気を配ったのは，数直線です。
基準となっている元の数から，「大きい場合は右へ」。
「小さい場合は左へ」とテープが伸びるようにプログラムしました。
左右どっちにテープが伸びるか。
これがなかなか重要なところなのです。
通常の感覚では，「大きい」と記されると，図体が大きいとなります。
「５大きい」と言われれば，元の状態より５だけ見た目が大きくなるのが，通常の感覚です。
でも，算数にはこういう日常的な感覚を受け入れない世界があります。
数直線は，まさにその世界です。
数直線は左に小さい数，右に大きい数を表す約束になっています。
ですから，右に行けば行くほど大きく，左に寄ればどんどん小さくなります。
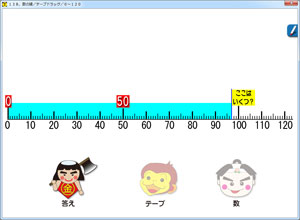その理解ために，９３というのは，「０から９３までの長さ（量）」を表していることを理解しておく必要があります。
それを『子どもが夢中で手を挙げる算数の授業』（１年２巻）に収録されている「１００までの数」ソフトで十分に理解していることを前提に，このソフトが作られています。
元の数から見て，「５大きい数」というのは，元の数から右に５めもり分移動した位置。
元の数から見て，「３小さい数」というのは，元の数から左に３めもり分移動した位置。
数直線上での「大きい」「小さい」の感覚を学べるようにと作り込んだのがこのソフトです。
中学で「９３＋（＋５）」や「４５＋（－３）」といった数の計算を学ぶときも数直線で思考します。
学年はかけ離れていますが，考え方は通じています。
数学に通じる学習を，１年生から視覚的にしっかり学べるのです。
大きな力が付きます。
有り難いです。
近日中に，もっと算数サイトにアップします。
御活用ください。
『教師の道標（みちしるべ）』から取り出した名言です。
－－－－－－－－－－－
人はやろうと思わなければ，
箸の一本も
動かすことは出来ない。
－－－－－－－－－－－
全く，その通りです。
この言葉は夏目漱石です。
漱石の言葉かと思うと，響きが大きくなります。
「しない」ことと，「できない」ことの違いを示した名言は江戸時代の古典にも出てきました。
そこでも感動しましたが，漱石の言葉でも，やっぱり感動します。
「しよう」「やろう」と思うこと。
それを本人がそう思うこと。
これが原動力なのです。
『教師の道標（みちしるべ）』には漱石の金言が紹介され，それに通じる実践の話しが紹介されています。
漱石の言葉を数回繰り返して読み味わい，それから本文を読みます。
金言効果が読書にも出ます。
実践が良い感じ響いてきます。
同様に，実際の教室でも金言を交えたら，どうなるでしょう。
子ども達にもきっと響きが大きくなります。
見開き２ページに金言が出てくる『教師の道標（みちしるべ）』を今読み返しています。
味わい深い教育書です。
