算数ソフトを使っている木島先生から，嬉しい便りが届きました。
ご紹介します。
－－－
ソフトの内容ですが、大うけは「スィート。ポテット。」でした。
わかりやすさは、面積のところです。複雑な図形の求積問題が、色を変えて示してくれていて、補助線も入るので、視覚的にわかりやすくなっていました。
考え方も１から３まで説明があり、よくわかりました。
求積問題の二つ目だったと思います。補助線を引いていくつかの図形に分けて足し算で答えを求めるようにすると、非常に面倒でミスしやすいという方法を考え方の１と２で示してありました。考え方３では、全体からその長方形の部分だけを引いて求めるという考え方を示してありました。
子どもたちに余計な説明をせずとも、問題によっては引き算で求めるやり方の方がシンプルでわかりやすいと自分たちで気づいていました。
彼らは足し算大好きですので、何でも足し算で求めようとします。いい気づきになるような工夫をしてくださっているのが、よくわかります。
１平方キロメートルの広さを理解させる画像も助かりました。何と言っても大阪城の広さには、私も驚きました。
今日も算数の授業で使わせていただきます。
－－－
算数ソフトを使って，「大受け」もあれば，「わかりやすさ」もあったのです。これだけでも，十分にすばらしい授業となります。
さらに，「説明をせずとも」「自分たちで気づいた」のです。これはハイレベルです。木島先生の指導力にソフトを加えるだけで，授業がぐっと変わってくるのです。
木島先生のメール，中嶋先生のブログ。両方に共通しているのは，「説明をしない」です。先生が説明をしなくても，子ども達が気づいてくるのです。
ここには，とても重要な指導の論理が横たわっています。
簡単に言うと，「バラバラ」から「まとまり」の展開です。「不整合」から「整合」への展開です。
ソフトを見たときは，初めての現象なので，個々がバラバラに認識されます。個々の関係がつかめないので，頭の中が「なにこれ？」「どうして？」といった状態になります。
それを複数回見ているうちに，個々の関係性が次第につかめ，ついに「なるほど！」「そういうことか！」と，「一つのまとまり」として見えるようになります。
バラバラだった事象を一つのまとまりとして認識すること，これが算数における「わかる」の過程的構造なのです。
４＋３＝７
この式の読み方は２種類あります。
Ａ ： ４たす３は７
Ｂ ： ４と３を合わせると，７になる。（７と等しくなる）
ＡＢに若干の違いがあります。
Ａの読み方は誰もが同じです。しかし，Ｂは人によって多少言い回しが変わります。
こういうＡＢの読み方を持つ文は他にもあります。身近なのは英語です。
I love you.
Ａ ： アイラブユー
Ｂ ： 私（おいら）はあなたが好き。（愛している）
Ａの読み方は誰もが同じですが，Ｂは状況によって多彩です。
どうして，「式」と「英文」が同じ構図になっているのでしょうか。もともと，式は西洋から入ってきた書き方なのです。西洋の言葉の文法に則って記されている，一種の文なのです。
英語で「４ and ３ are ７」とか「４ plus ３ equals ７」という言い回しが，そのまま「４＋３＝７」になったのです。
つまり，Ｂは西洋文法の式を，日本語に翻訳して言い直しているのです。
と，このように書いても，今ひとつわかりにくいですね。
私たちは，英語と文法の似た漢文を勉強してきています。漢文はそのままでは読みづらいので，返り点をつけて読みやすくしてきたことを，高校で学んできました。
漢文の返り点を使って式を書いてみます。ＡとＢの関係が見えてきます。
式に出てくる文字の順番を入れ替えて読んでいるのが，Ｂなのです。
「式は日本語に帰化した西洋の文」なのです。「３」や「４」などの算用数字も明治になって広まった外来の文字です。外来の文字を使った式は，さらに西洋文法の形を保ったまま，日本に吸収され，今や完全に帰化しました。
ですから，式を見てもその文字の配列に違和感を感じる人はいません。私も違和感を感じません。すっかり帰化した状態で学んできたからです。
大人に違和感が無くても，学びはじめの子ども達の中には，違和感を感じる子がいます。式の文字配列は，子どもにとって普通の文の書き方と違いすぎ，面食らうからです。これは，分数を下から上に書くのと似ています。３年生ですら，分数の習い始めに，分母を上に書いてしまう子もいます。分数より複雑な文字配列の式です。１年生の式の学習には，ちょっと工夫が必要となります。
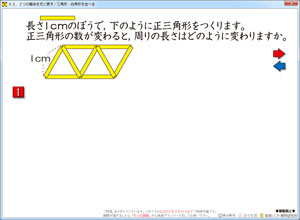三角形を「棒」で作り直しました。
設問が，「三角形の数」と「周りの長さ」の関係の把握ですので，辺を強調して数えやすくすることが，理解を助けることにつながると考えたからです。
さらに，色も変えられるように配慮しました。
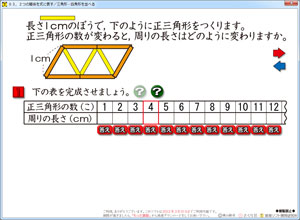ボタンクリックで，このように色が変われば，「周り」がどこなのか，一目でわかります。
それでも，「変化の関係」を把握できるかどうかは，疑問です。そこで，さらに，色が変わり，これならわかるだろうという色つけをしました。
２つめの「？」ボタンをクリックするとそのようになります。
このソフトも，「もっと！算数」サイトにアップします。
どのように色がつくか，是非ごらんになっていただけたらと思います。
昨日ご紹介したのは，中嶋先生のブログです。
算数ソフトを使って授業をしたら，９０点が１名，他の子は全員が１００点だったのですから，これはびっくりです。
今日は，山本先生のブログをご紹介します。「もっと！算数」サイトにアップしてある２年の分数のソフトを使っての授業です。その様子は・・・
－－－－－
「１/４」は長方形を扱ったところで時間になったので終了。
「続きは明日もう一度やろう」というと，再び「やったぁー」の声。
（詳しくは → http://star.ap.teacup.com/mymmtuba/757.html ）
－－－－－
算数を明日やると言って，「やったー」と歓声が上がることに驚きます。通常は，「えーっ！」です。この「えーっ」を，「やったー！」に切り替えるには，かなりの準備が必要です。準備なしの時は，かなり知恵を絞って子どもをその気にさせる努力が必要です。算数を盛り上げるのは，それぐらい大変なことなのです。
そういう特別な努力や大変な工夫をすることもなく，ただ算数ソフトを使って授業を進めただけで，子ども達は明日も算数をやりたがるのです。うれしいじゃありませんか。
ブログなどに算数ソフトを使った記事を見つけたら，また，お知らせをします。
算数ソフトを使って算数の１単元を授業をされた先生のクラスの出来事です。
ブログから一部引用します。
－－－－－
先日、市販のテストを行いました。
結果を見て、ビックリ仰天！
何と、一人の子が９０点。他の子は全て１００点という結果が出ました。テストの裏の５０点満点の問題も、一人を除き、５０点満点です。
しかも、子ども達の中には、特別支援学級に通う子が一人いるのですが、その子が１５０点満点という結果！
－－－－－
驚きます。
算数ソフトをどんな風に使ったら，このようなすばらしい成果を上げることのが出来るのでしょうか。何か，特別な使い方が必要なのかと思います。でも，違いました。
－－－－－
算数ソフトを繰り返し見せて考えさせる、何度も何度も考えさせることによって、全ての子が完全に理解してしまいます。教師の説明無しでです。
－－－－－
まさに，ここが新しい指導法です。先生が説明するのではなく，子ども達が「そうか！」とわかる瞬間が来るまで何度もソフトで考えさせることです。
こんな風に書くと，強引な授業をしているように感じてくるかもしれませんが，算数ソフトを使って算数の授業をすると，子ども達は盛り上がり，やる気満々になり，どんどんわかろうとしてきます。
この積極的な姿勢が下支えになっているので，何度も何度も考えさせても，大丈夫なのです。
詳しくは，↓をごらんくんださい。
http://shikarikata.blog.fc2.com/blog-date-20110226-1.html
「算数ソフト」というのは，『子どもが夢中で手を挙げる算数』（さくら社）のことです。
前回の続きです。
４年生の「変わり方」のソフトを開発しています。前回も書きましたが，「どんな風に変わっていくのか，それを考える単元」なのですから，変わる様子を見て規則性を見いだすことが大切なのです。
「変わる様子を見る」には，次の２つの「見る」があります。
１，複数の「変化物」を見る
２，「変化物」の変化の様子を見る
「変化の規則性」を見いだすには，「変化物」を複数見て，「どうもこの手のものは足し算の規則性がありそうだ」「これは，かけ算の規則性がありそうだ」と一般化していく力を持たせることが，私は大切と思っています。
そのために，ソフトに「変化物」を３つは盛り込みたいと思っています。
変化の規則性を「面白い！」と感じ取れる子がたくさん出てほしいですね。
ここは頑張らねばと思います。
