５年生で学習する「帯グラフ・円グラフ」
この単元で算数ソフトを使っている渥美先生から，とってもうれしいメールをいただきました。
－－－－－－－－－－－－
言いたくて仕方が無くなる。
聞きたくて仕方が無くなる。
こういう状態になります。
－－－－－－－－－－－－
マウスでクリックしていると，子ども達が「言いたくて仕方がない状態」になるのです。
答えも言いたいし，どうしてなのかも言いたいし・・・
そんな嬉しい状態になるのです。
普通の授業では，いつも決まった子ばかりが手を挙げがちです。
時々，違う子が手を挙げると，その子を優先して・・・・。
あの子にもこの子にも，もっと手を挙げて欲しいあぁ・・・と思います。
そういう状態が，算数ソフトを使うと一変します。
子ども達がやる気満々になってくれるので，先生の話もとても良く聞いてくれます。
「もっと知りたい！」という気持ちになっていきます。
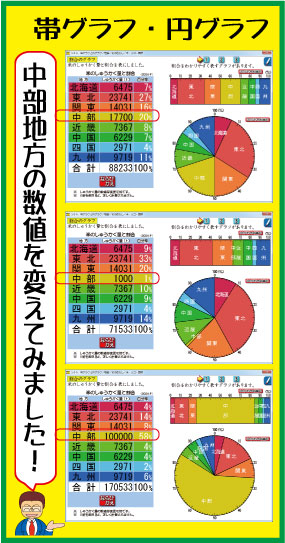例えば，ソフトの中の中部地方の数値をちょこっと変えてみます。
何も変えないときの中部地方は「１７７００ｔ」。黄土色のところです。順位は第２位。
この数値を，わざと「１０００ｔ」に減らしてみます。
すると，どうなるでしょう。割合は１％ですから，帯グラフも円グラフも狭くなります。順位はビリです。
今度は，「１０万ｔ」に増やしてみます。
すると，５８％にもなります。中部地方のグラフは広くなり，順位は１位へと変わります。
こんな風に２回，３回と変更してみて，それから子ども達の希望に合わせて，１つの地方の数値を変更したら，どうなるでしょう。
「広くなる！」「狭くなる！」
「○○地方と同じぐらいになる！」
「○○地方の２倍ぐらいになる！」
あれこれ，言いたくなりますよね。
人間は不思議な生き物で，ある程度の理解が進むと，そのことについて言いたくなってきます。
「ある程度の理解」に達する前だと，妙に口ごもります。わざと知らない振りをすることもあります。
それが，ちょっと分かってくると，気持ちが動き始めます。
かなり知った状態になると，一言も二言も言いたくなります。人によっては，つい口走ることすらあります。
学習の大事なポイントは，この「ある程度の理解が進む」状態にまで，トントンと進めることです。それには，２回，３回とやってみせることです。
繰り返されると，そこにきまりが見えてくるので，あれこれ見えてきて，次第に言いたくなってくるのです。
ここを１回目から考えさせようとすると，頭が動きにくくなります。授業も重くなりますね。
－－
このソフトは，『子どもが夢中で手を挙げる算数の授業』の５年２巻に入っています。
６年生の「速さ」。
この単元の基本といえば，５０ｍを８秒で走ったとか，４０ｍを７秒で走ったという記録です。
この単元は，「単位量当たり」という考え方の流れを汲んでいるので，これを普通は「１秒当たり」の秒速で比べます。でも，考える力を高めるためたい場合には，「１ｍ当たり」で比べることもできることを学んだ方が良いです。
「１秒当たり」「１ｍ当たり」。
この両方の見方を分かりやすく表現するときに，役立つのが線分図です。
でも，どうやったら，その「分かりやすさ」を示せるのでしょう。それが頭の使い所です。
私の雰囲気ですと，道のりの方から動き出すのが「１ｍ当たり」。時間の方から動き出すのが「１秒当たり」という感じにすると，少し分かりやすくなるかなと思っています。
でも，こういうのは，実際に付くって動かしてみないと感触がわかりません。
今週中には作り進めて，現状の言葉で理解する状態よりは１歩も２歩も分かりやすいソフトに仕上げたいと思っています。
ところで，「速さ」という概念ですが，これを考えついたのは，万有引力で有名なあのニュートンです。時間と空間を結びつけて考えたのです。ニュートンは算数・数学でも偉人です。
「チーム・奇跡の算数」の続き。
中田先生から，５年生の「図形の面積」の指導案が提案されました。
よく考えられていて，この授業なら子ども達の頭はフル回転すると感じました。特に，導入は興味をかき立てる形になっていて，上手いなと思いました。
中田先生の授業でもソフトが使われました。そのソフトは，教室プレゼンターを使って算数ソフトを開発し続けている種市先生が作られたものです。いつかはお会いしたいと思っている先生のお名前が出て，とても身近に感じられました。
学校の先生をやりながらソフトを開発するのはとても大変です。特に，マウスドラッグで図形を動かすのは，なかなか面倒で手間がかかります。 そこが作り進められないと伺ったので，私の方でも作ってみることにしました。
中田先生とのコラボソフトです。
右をご覧の通り，三角形の頂点をドラッグして，頂点を動かすことができます。
これが，「等積変形」です。面積を変えずに形だけを変えることです。
大切な概念なので，面積の授業では子ども達にしっかり見せたいのですが，思うように見せられないところとなっています。
面積を保存したまま，形を変えるのが「等積変形」。
これと同等に大切な見方があります。形を保存したまま，位置を変える「等積移動」です。
等積移動には，「平行移動」「回転移動」があります。
このソフトには，「回転移動」の機能も付けています。
左下に小さな４つのボタンがあります。これが回転移動をスタートさせるボタンです。どんな風に回転するのでしょうか。ソフトがアップされましたら，ダウンロードしてご覧になって下さい。
このソフトを使って，白と水色の部分の面積が等しいことを学びます。
等積変形を何度も見て，回転移動で等しさの確認ができるように作られています。
ここまでつくってあると，見ている内に，等しくなる理由（言い換えれば，「等しくなることの論証」）を言いたくなってきます。教科書の画像を見ているだけではできない，質の高い授業ができます。
おまけの機能が付いています。
長方形の中のどこか好きなところをクリックすると，頂点がクリックしたところに瞬間移動します。好きなところをクリックすると，そこに頂点ができるのです。
これが，数学でよく登場する「任意の１点」をとる行為です。
任意の１点について，子ども達が「どこでも点」と言っていたことを中田先生が話してくれました。こういう重要なところを聞き逃さず大切に扱う所，さすがだと思いました。
数学用語を平易に言う言葉を，「辺」を「へり」，「頂点」を「かど」などのように，固定化することが学習として大切です。これから先，私は「任意の１点」を「どこでも点」として使っていきたいと思います。
★図形のソフトは，近日中に，もっと算数サイトにアップされます。
円グラフの勉強が，モーレツに楽しくなりますね。
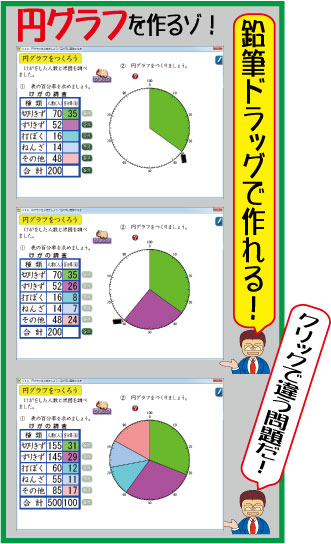
『子どもが夢中で手を挙げる算数の授業』 （５年の２巻）の「割合と円グラフ・帯グラフ」の中に，右のソフトが入っています。
ファイル名は，「１３Ａ，円グラフをかきましょう／百分率は整数になる」です。
ご覧のように，表を見てグラフを作る学習専用に作られたソフトです。
ファイル名にあるように，１３Ａのファイルは，「百分率は整数になる」タイプだけが出題されます。計算が簡単ですので，取り組みやすいです。
基本に忠実に，しっかり計算できるようにします。
お楽しみは円グラフづくりです。鉛筆をドラッグすると，半径が開き始めます。「ここだ！」というところでマウスを放すと，正誤判定されます。
合っていれば，右のように部分グラフができます。間違っていたら鉛筆が元に戻ります。
ここを先生がマウス操作するときは，「ここだ!」と言う所で，「ボンバー！」などと声を出させるのも楽しいです。
ものすごく盛り上がります。
子どもがマウスを操作しても，グッと楽しくなります。
心配性の先生は，子供にやらせて，そこで間違えたら・・・と思います。
楽しいときは，あんまり心配しない方が良いです。
本気で間違えても，「アレッ!」と思って，自己修正を始めるからです。それをニコニコしながら待っていれば良いのです。
そうして，「来年，ここを習う子に，気を付けるところを教えるとしたら，それは何か」を考えさせれば，自分が間違えたところが，「生きて活用できる情報」となります。
楽しい雰囲気が作れると，授業はいろいろな姿で進行できます。
先生のお得意の姿でぜひ進めてください。
ソフトを持っている先生は，良い気持ちで授業ができますね。
子ども達も幸せってものです。
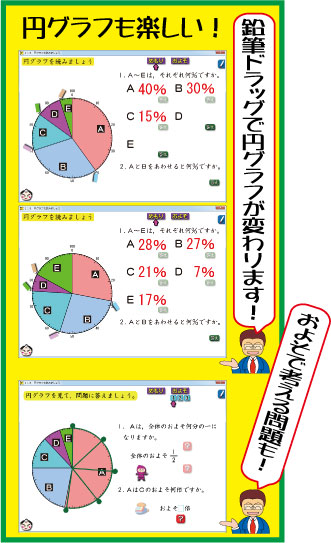『子どもが夢中で手を挙げる算数の授業』５年生２巻に，「割合と円グラフ・帯グラフ」が入っています。
その中の「１１Ｂ，円グラフを読みましょう」が右のソフトです。
円グラフを見て，まず，ＡＢＣＤＥがそれぞれ何％なのか答えます。
次に，ＡとＢを合わせると何％になるか答えていきます。
円グラフの周りに，鉛筆が付いています。算数ソフトを使ったことのある先生でしたら，この鉛筆を見ただけで，ドラッグしたくなります。ドラッグに合わせて，きっと，円グラフの半径の傾きが変わるのだろうと感じます。
全く，その通りです。
先生が鉛筆をドラッグしても良いですし，円グラフが大好きになった子にドラッグチャンスを与えることもできます。
２，３人にやってもらったら，次は「円グラフが得意だ！」という気持ちになった子に，ドラッグチャンスを与えるのも良いですよね。
やる気満々になってきます。
そうして，目盛りを正しく読めるようになったら，右上にある「およそ」ボタンを押して，「全体の何分の一になっているか」「ＡはＣの何倍か」など，ざっくりと目測で考える勉強に入ります。
算数の勉強というと，精密な方向へ進むように思えるのですが，意外にも，精密に正しく理解できるようになったら，ざっくりと見ていく方向へ進みます。
上の何分の一か，何倍かというような「目分量」がその一つです。
なんで，こんな学習をするのと不思議に思う先生もいるようですが，これは頭の切れ味を良くする学習なのです。
グラフを見たとき，正確な読み取りが必要な場合もあれば，大筋の把握で良い場合もあります。その時の目的によって，さっと対応できる頭を持っていると，「できる！」ということになります。
両刀遣いという感じです。
また，大雑把に読んでも，正確に読み取る力がないと，中身が空っぽの読みとなります。
正確に読める力を押さえて，「この場はざっくりと」と場に応じて読む人は，中身がしっかりしている人となります。
正確さと大枠。この両方をしっかり学べる単元です。ソフトも使って楽しくしっかりと学んで欲しいです。
右の図をご覧下さい。
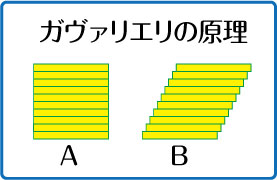
同じ長さの細長い板を１０枚ずつならべています。
Ａは真っ直ぐに並べていますが，Ｂはちょっとずつずらして並べています。
さて，どちらの面積の方が広いのでしょうか。
このように問われても，どちらかが広いとは思えません。広さは，重なってさえいなければ，並べ方によって左右されないからです。
ガリレオ（１５６４～１６４２）の高弟だった，１７世紀のイタリアの数学者ガヴァリエリ（１５９８～１６４７）は，それまでの数学の考えを進め，「面は幅のない線の集合」と考え『不可分量の幾何学』にまとめました。
この考え方は，頭が柔軟になります。Ａのカチッとした面積が自由自在に動き出すような気持ちになってくるからです。
ですので，『不可分量の幾何学』には，いったいどんな風に書いてあるのか気になります。読んでみたいと思うのですが，こういう本の翻訳本があるのかどうか，それすら分かりません。
今，小学校で教えている方法は，面積を辺でがっちり固定して見る方法です。ですので，見た通りにしか図形が見えてこない頭になっていきます。これは，教える先生も同じです。
これをガヴァリエリのように，積み重ねているという形でも扱うようになったら，高さが同じなら途中はどんな状態でも関係ないことがわかります。自由にスライドさせてもかまわないと頭が働くようになります。
こういうソフトを，いつかつくって，面積の発展的な見方として見てもらえたら良いなぁと思っています。しばらくは，作れませんが・・・。
