Category Archives: 算数

チーム算数が開催されました。
城ケ崎先生と押田先生と私の３人です。

一番面白かったのは，城ヶ崎先生が一般参加したセミナーでの出来事でした。
話し合い活動があったようで，それにまつわる話をしてくれ，非常に納得しました。

私は，スクーで話した，帯分数の歴史を話しました。
そういう話をしていたら，押田先生も城ヶ崎先生も，「歴史」が大事なんだと話してくれました。
特に押田先生は，「算数の歴史」を知りたいし，子ども達にも伝えたいと語っていました。
小学校の先生の視点で，「算数の歴史」がまとめられたら，これは貴重でしょうね。

今回のメインの話は，「習慣は第二の天性」の話です。
この言葉がドンピシャで適用されているのが，算数なのです。
単元事に，この第二の天性作りがされている大変珍しい教科が算数なのです。
それを簡単な図にして示しました。
その図は，パッと見，「否定の否定」の発展的構造図とも言えます。

「習慣は第二の天性」の事例として，大分の幼稚園の先生にしたように，チーム算数でも「指折り１０まで数える」話をしました。

そうして，私が今読んでいる本を紹介しました。
『数の歴史と理論』です。
この本，まだまだ読み始めなのですが，数の本として非常に質が高いです。
何しろ，「４本」とか「２人」という助数詞の背景が記されています。
もう，これだけで，１０冊分ぐらいのパワーを感じます。

すばらしい内容が書いてあるのですが，古書のため，本を開くと，古書の香りがただよいます。
ですので，よほど空いている電車の中でないと，開くことができません。
そこが，ちょっと残念ですが，実にいい本です。

スクーで，算数の話を４本しました。
「１か９分の８は，１なのか，８／９なのか？」
「分母・分子から古代中国を覗く」
「世阿弥も分数を活用していた」
「形式分数って，なんだ」

どの話も面白く語れました。
そうして，最後に，
「日本最古の分数は神社への勅」
という話をする予定でしたが，ちょっと時間が来てしまし，お話しできませんでした。

その話を，ここに書き記しておきます。
－－
「日本最古」というのは，文献に残っている最古です。
それも，私が読んだ範囲です。
ですので，これからご紹介する分数より，もっと昔に記された分数が出てきたら，この話は第2位，第3位と，順次繰り下がっていきます。

私が発見した最古の分数は，『日本書紀』に出てきます。
天武6年（672年）の事として，ご覧のように登場しています。

己丑（つちのとの　うしのひ）に，天皇の勅（みことのり）がありました。
神社の神税（かむちから＝税金）は，
３つに分けて１つを神につかえるために使い，
２つ分は神主にわけましょう。

集められた税金の分け方が記されていたのです。

この少し後に，もう１カ所，分数が出てきます。

乙巳（きのとの　みのひ）に，天皇の詔（みことのり）がありました。
上戸（かみつへ）には，１町を与えましょう。
中戸（なかつへ）には，半町を与えましょう。
下戸（しもつへ）には，４分の１町を与えましょう。

宅地の分け与えで分数が登場しています。

途中，点々で省略しているところには，次のように出ています。
右大臣に賜う宅地四町。
直広弐より以上には二町。
大参より以上には一町。

分数が出てきた下戸は，わずか１／４町です。
「下戸」という言葉の持つ語感と，最後に示されている順序などから，
かなり狭い宅地なんだろうなと思います。

ところが，ところが・・・。
１町というのは，かなり広いのです。
どのくらいの広さかいうと，４００尺四方の土地が一町なのです。
１尺は約３０ｃｍ。時代が違えば寸法に多少の違いがあるかもしれませんが，
おおむね３０ｃｍと考えてみると，１町は１辺が１２０ｍの正方形となります。
１２０ｍ×１２０ｍ＝１４４００平米です。
これを坪に直すと，４３６０坪ぐらいです。
ちょっと控えめに，４０００坪としても，下戸はその１／４ですから，１０００坪の宅地となります。
下戸は，漢字で見るより実に身分が高いと実感します。

天皇のみことのりには，２種類ありました。
「詔」と「勅」です。
「詔」は主に大臣に向かって出されるお言葉です。
「勅」は国民に向かって出される天皇のお言葉です。
宅地の方の「みことのり」は「詔」なので，下戸と呼ばれていてもとっても偉かったのです。
－－
こういう話をして，スクーの話をおしまいにする予定でした。
また機会があれば，お話をしたいと思います。
ご静聴，ありがとうございました。

※私の読んでいる『日本書紀』は岩波文庫の本です。とても，勉強になるいい本です。

今度の日曜は，スクーです。
「横山験也の算数の授業」が生放送されます。
お時間のある先生，是非ごらんください。
－－
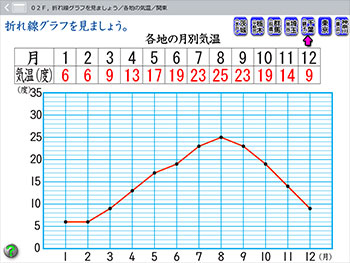４年生の「折れ線グラフ」の「０２Ｆ、折れ線グラフをみましょう／各地の天気／関東」のソフトです。

折れ線グラフって，どんなグラフなのか，その様子を見るためのソフトです。
各地の気温のグラフを見せて，感想を語り合うのも良い勉強になります。
なにしろ，グラフを補助する表も載っているので，数字での把握ができます。
数を伴った感想が出てくれば，それは質の高い感想となります。

このソフト，ちょっと工夫すると，面白い現象を見ることができます。
「自分の県を中心に，他の県をみる」という見方ができます。
たとえば，私は千葉県なので，まずは千葉県をクリックします。
すると，ご覧のように千葉県の平均気温の表とグラフが出てきます。
次に，茨城をクリックします。
すると，グラフが千葉から，茨城へとジワーンと変化します。
折れ線の両端が下がっていく様子がわかります。
どうも，千葉の方が暖かいとわかります。

また，千葉をクリックします。次に栃木をクリックします。
栃木も折れ線の両端が下がっていく様子がわかります。

こんな風に，自分の県を見てから，他の県を見る。また，自分の県を見てから，他の県を見る。
これを繰り返していくと，近隣の県との微妙な違いに気がつきます。

そうして，重要なのは，その微妙な違いは「折れ線」だとよくわかるが，「表」ではよくわからないことです。
「折れ線」と「表」。
両方が表示されていますが，パッと見て変化がわかるのが「折れ線グラフ」の特徴だと実感的にわかります。
－－
『関大初等部式　思考力育成法』
小学生がベン図を使って思考するなど，驚きの連続です。

工藤先生から，「算数ソフトキャラクター解説」第２号をいただきました。
今回のは，６年「比」、「比例」「おこり得る場合」です。
算数ソフトファンの皆さんには，授業の様子が思い出されてきますね。

さて，工藤先生の解説をご紹介します。
－－－－－－－－－－－－－－－－－－－
①・「クリックしてくだ青サイ」
０１号にて紹介した「クリックして赤サイ」との違いは、
右向き、別数字表示、次の作業を誘導するという点。

②・「クリックしてくだちょうちんアンコウ」
クリックシリーズの別キャラ。
いくつかの数字をまとめて変更する際に登場。

③・「歴史キャラ連合」
色々な単元に登場する、歴史キャラ連合。
歴史の学習と絡めると２倍おいしい。しかし、深追いすると時間がかかる。
聖徳太子、藤原道長、清少納言、源頼朝などそうそうたるメンバーが勢揃い。

④・「順数字」
とっても地味な表示キャラ？ではあるが、とっても大事な順番を表し、
順を追って作業の手順ややり方、注意ポイントなどをおさえる。

＠＠　おまけの隠れキャラ　＠＠
⑤◇「よっしゃー！」
よっしゃー！というかけ声と共に出現。
その名もそのまま「よっしゃー！」だが、さてどこに出てくるでしょうか。

◇「いよー！」
画像の表示はないが、量や数字が増えたり減ったりする際の効果音。
他のことに気をとられ脇見をしていたやんちゃ君も、この音一つで画面に大注目。

◇「歌舞伎音」
画像の表示はないが、量の変化などの際に鳴り響く歌舞伎的な効果音。
間をとるにも最高。子ども達の中にはリズムをとる子もいたりする。
－－－－－－－－－－－－－－－－－－－－－－
楽しい内容がざくざくですね。

中でも，感動的なのは，１つめの◇の２行目です。
「他のことに気をとられ脇見をしていたやんちゃ君も、この音一つで画面に大注目。」
何か，他のことに気をとられること，誰にでもありますよね。
そんなとき，「こっちを見なさい」と言いたくなりますが，効果音が聞こえて，さっと学習に戻ります。
こういうのスマートですよね。

また，２つめの◇も良いですね。
「子ども達の中にはリズムをとる子もいたりする。」
子ども達の心をつかんでいますね。
これこそ，「楽しい」という状態です。
孔子の言葉（論語）に，こんな言葉があります。

子曰く，
これを知る者は，これを好む者にしかず。
これを好む者は，これを楽しむ者にしかず。

知っている人は立派ですが，それを好んでいる人にはかないませんね。
好んでいる人もすばらしいですが，それを楽しんでいる人にはかないませんね。
というような意味です。

まず，楽しんで取り組めるように工夫することが，学習の第１の要件です。
算数の授業に算数ソフトを活用している先生のクラスは，この第１要件が満たされていますね。

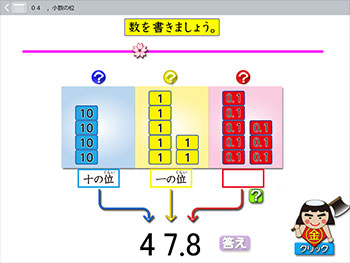３年生の小数のソフトです。

１０のカード。
１のカード。
０．１のカード。
それぞれが，位のコーナーに入っています。
それを見て，いったいどんな小数になるのか，答えていくソフトです。

これを実際にカードを使って授業をしたら，大変だと思います。
大変な上に，授業のテンポがもたもたします。
右の４７．８を出題するには，４＋７＋８で，合計１９枚のカードを黒板に貼り付けることになります。
結構な時間がかかってしまいます。
何問も出すのは，なかなか大変ですね。

それがクラウドをポンと立ち上げると，この問題がクリック一つで出題できます。
パッと問題が変わるので，子ども達も真剣に見て，さっと答えようとします。
このスピード感。意欲を高めます。

数回問題を出すと，素早く答えられるようになってきます。
そうなったら，「１０問連続，気合いで答えよう！」などと出題することもできます。
ちょっとしたスピードアップは，子ども達も大好きです。
チャレンジ精神に火がつく感じになります。

もう大丈夫となったら，次につなげる出題をしてみるといいです。
クリックして，問題が出たら，すぐには答えず，次のように言わせます。
「１０が４こと，１が７こと，０．１が８だから，４７．８です！」
示されている仕組みを言葉にして言わせる学習です。
すると，そういう文章で示された問題への抵抗もぐっと少なくなります。
言い回しになれることもありますし，意味を言葉としても理解できる力がつくからです。

青・黄・赤の「？」ボタンがあります。
これは実に重要です。
「赤？」をクリックすると，０．１が１つずつ増えていきます。
０．１が９になったとき，「さて，もう１回，赤？をクリックすると，どうなるでしょう？？？」と聞いてみましょう。

クリックすると，１が１つ増えて，０．１が全部無くなります。
繰り上がるのです。
この繰り上がっていく様子も，算数としては重要なポイントです。
位取りで表されている数の持っている，実に面白い仕組みなのです。
何度か見ることで，数の概念がまたひとつしっかりしてきます。
－－
先ほど書いた，「仕組みを言葉にする学習」は，意外と重要なところです。
ソフトを使うと，この方面の指導も繰り返しできるので，効果的に行えます。
かけ算九九の「仕組み言葉学習」について，
７月に開催された「事前学習法説明会ｉｎ千葉」で上澤先生と藪田先生にお話ししました。
両先生，感動していました。