チーム算数の定例会。
今回は４名です。城ヶ崎先生，中田先生，押田先生と私。
スタートは算数ソフトの新作発表。
神奈川の佐藤先生が平均点で９７点をとるに至った授業で，活躍的に頑張った分配法則・結合法則・交換法則のソフトなどをお見せしました。
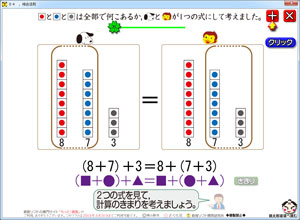この３つの法則は，これまでの算数とはひと味違う，ちょっと数学が入り込んできている学習です。
右の画像を見ていただくと分かりますが，■や●や▲を数の代わりに使って，「こういう事が言えるね」と学ぶところです。
この■●▲が，後々のaでありbなのです。
そうです。ご存じ「代数」の世界です。
この文字や記号を使って考えるということは，これまでの算数と何が違うのでしょう。そこの理解があると，この学習はもっともっとしっかり教えたいという気持ちになります。
これまでの算数は，「具体から離れ，数で考える道」だったのです。
リンゴが５こあって，隣を見たら，また５こあって，手元を見たらそこにも５こあって。
これを１こ，２こ，３こ・・と数えても合計を知ることができます。でも，それじゃあ，ちょっと頭が足らないような気がします。計算を知っている人には，それが強く感じられます。
そこで，覚えてしまえば楽に合計を知ることができる画期的な方法として，「たし算」とか「かけ算」をしっかり学習させるようになっています。
そうして，その恩恵がかなり分かってきた頃，「そろそろ次のステップに行きましょうか」とお誘いをしてきているのが，この■●▲たちです。
「数から離れ，記号（代数）で考える道」へ誘っているのです。
具体から離陸して，数の世界へ。
その数の世界から離陸して，代数の世界へ。
この離陸するときに大事なことは，量をこなすことです。
量をこなし，頭でも体でも馴染むところまで進まないと，「その場理解」で終わってしまい，翌日には，さて何の事やらとなります。学ぶ子ども達にとっては，なじみのない考え方の世界だからです。
そんな第２回目の離陸単元で，佐藤先生は平均点で９７点を出しました。
使ったソフトが量をこなせるように作られているので，子ども達の様子を見ながら，離陸できるまで指導を繰り返すことができたのです。きっと，佐藤先生は一人一人のお子さんが「ほぼ確実」になっても，「もう一押し！」と，「押さえの繰り返し」指導をされたのだと思います。子ども達の様子から，あとどの程度繰り返せばよいかを見抜く力があったのでしょう。そういう教師力が，これからの算数には必須の力となります。
－－
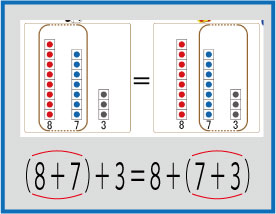
ところで，上の画像の図の部分ですが，ここの工夫は自分でもお気に入りの所です。
図を囲っている線，縦は実線なのですが，横は点線になっています。括弧をイメージしています。
ここまでは，ソフトを見た先生なら，すぐに気付きます。
ですが，この点線の重要性にはなかなか気付きません。 それは，括弧は「弧で括（くく）る」と書いてあるように，円の弧で括られているのです。ここから考えれば，もしかしたら，原始的な雰囲気として「８＋７」や「７＋３」をぐるっと括っていたのを，その左右両端だけを残して表記しているのではないかと思えてきます。
ここまで思えてくると，その先，ちょっと発展させることができます。
小学校では小括弧しか出てきませんが，中括弧・大括弧も，ぐるっと括ってみると，「囲みの中から外に向かって計算する」 という規則が分かってきます。その囲みは必ず入れ子状態になっている事にも気付きます。
括っている記号にこういう原理があるのでないかと思うと，似たような物として，文章のカギ括弧があることに気になってきます。カギからカギまでを括ると，マンガの吹き出しのようになります。
また，二重括弧と，ただのカギ括弧。これも，算数の括弧同様，必ず入れ子状態になります。
最初に紹介したソフトのところで，このような話しになり，ついには，句読点を使わない文章の話しなど，話しは多岐にわたりました。面白かったです。
８月に発売になった『チャレンジ！学校クロスワード王ゴールド』（ほるぷ出版）が４刷りになりました。
ほるぷ出版さんから初めて本を出したのは，１９９８年の５月です。
『学校クイズ王１０１』という本で，当時，編集を担当してくださった会社の社長さんが，だれに小学生向けの学習クイズの本を書いてもらおうかと，書店を見て回ったそうです。そのころ，私は主婦の友社さんからその手の本を出していました。それが偶然，社長さんの目にとまり，お声をかけていただきました。
これが御縁となり，その後，毎年，児童書を書かせていただいています。
最初の本から,もう，１５年近く経ちます。その間に，ほるぷ出版さんから出させていただいた児童書の数は，なんと４５冊にもなります。
そうして，今も，今度はこんな本にしましょうとお話しを頂き，そこへ向けて少しずつ取り組んでいます。
学習クイズでは，朝日小学生新聞さんにもお世話になっています。２００１年から毎週１回，ある年は週に２回の連載を頂いています。この連載は，隅っこにちょっとというのではなく，広告欄を除く紙面１ページ分の分量がある大型の連載です。身に余る光栄と，ありがたく思っています。
子ども達が夢中になり，盛り上がる授業を研究してきた一つの成果と感じています。
チャンスがある限り，学習クイズの本を書き続けていきたいと思います。
円グラフの勉強が，モーレツに楽しくなりますね。
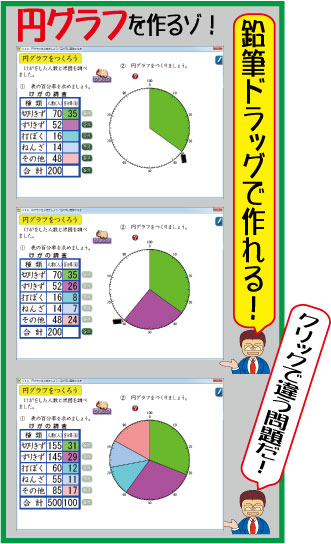
『子どもが夢中で手を挙げる算数の授業』 （５年の２巻）の「割合と円グラフ・帯グラフ」の中に，右のソフトが入っています。
ファイル名は，「１３Ａ，円グラフをかきましょう／百分率は整数になる」です。
ご覧のように，表を見てグラフを作る学習専用に作られたソフトです。
ファイル名にあるように，１３Ａのファイルは，「百分率は整数になる」タイプだけが出題されます。計算が簡単ですので，取り組みやすいです。
基本に忠実に，しっかり計算できるようにします。
お楽しみは円グラフづくりです。鉛筆をドラッグすると，半径が開き始めます。「ここだ！」というところでマウスを放すと，正誤判定されます。
合っていれば，右のように部分グラフができます。間違っていたら鉛筆が元に戻ります。
ここを先生がマウス操作するときは，「ここだ!」と言う所で，「ボンバー！」などと声を出させるのも楽しいです。
ものすごく盛り上がります。
子どもがマウスを操作しても，グッと楽しくなります。
心配性の先生は，子供にやらせて，そこで間違えたら・・・と思います。
楽しいときは，あんまり心配しない方が良いです。
本気で間違えても，「アレッ!」と思って，自己修正を始めるからです。それをニコニコしながら待っていれば良いのです。
そうして，「来年，ここを習う子に，気を付けるところを教えるとしたら，それは何か」を考えさせれば，自分が間違えたところが，「生きて活用できる情報」となります。
楽しい雰囲気が作れると，授業はいろいろな姿で進行できます。
先生のお得意の姿でぜひ進めてください。
ソフトを持っている先生は，良い気持ちで授業ができますね。
子ども達も幸せってものです。
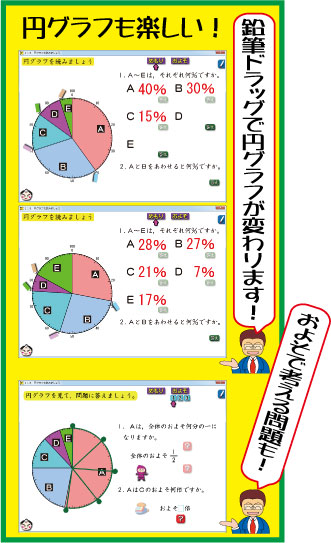『子どもが夢中で手を挙げる算数の授業』５年生２巻に，「割合と円グラフ・帯グラフ」が入っています。
その中の「１１Ｂ，円グラフを読みましょう」が右のソフトです。
円グラフを見て，まず，ＡＢＣＤＥがそれぞれ何％なのか答えます。
次に，ＡとＢを合わせると何％になるか答えていきます。
円グラフの周りに，鉛筆が付いています。算数ソフトを使ったことのある先生でしたら，この鉛筆を見ただけで，ドラッグしたくなります。ドラッグに合わせて，きっと，円グラフの半径の傾きが変わるのだろうと感じます。
全く，その通りです。
先生が鉛筆をドラッグしても良いですし，円グラフが大好きになった子にドラッグチャンスを与えることもできます。
２，３人にやってもらったら，次は「円グラフが得意だ！」という気持ちになった子に，ドラッグチャンスを与えるのも良いですよね。
やる気満々になってきます。
そうして，目盛りを正しく読めるようになったら，右上にある「およそ」ボタンを押して，「全体の何分の一になっているか」「ＡはＣの何倍か」など，ざっくりと目測で考える勉強に入ります。
算数の勉強というと，精密な方向へ進むように思えるのですが，意外にも，精密に正しく理解できるようになったら，ざっくりと見ていく方向へ進みます。
上の何分の一か，何倍かというような「目分量」がその一つです。
なんで，こんな学習をするのと不思議に思う先生もいるようですが，これは頭の切れ味を良くする学習なのです。
グラフを見たとき，正確な読み取りが必要な場合もあれば，大筋の把握で良い場合もあります。その時の目的によって，さっと対応できる頭を持っていると，「できる！」ということになります。
両刀遣いという感じです。
また，大雑把に読んでも，正確に読み取る力がないと，中身が空っぽの読みとなります。
正確に読める力を押さえて，「この場はざっくりと」と場に応じて読む人は，中身がしっかりしている人となります。
正確さと大枠。この両方をしっかり学べる単元です。ソフトも使って楽しくしっかりと学んで欲しいです。
友達の藤本浩行先生が新しく本を出しました。『信頼を勝ち取る「保護者対応」』（明治図書）です。
「はじめに」に，この本が誕生する秘話が記されています。
昨年，藤本先生がさくら社から出した『新任教師 はじめの一歩』を明治図書の編集の方が読まれ，それがきっかけとなって，この新刊が出ることになりました。
どんどん読み進めていったら，途中のコラムに私の本が紹介されていました。
「実践！ 家庭訪問のマナー」というコラム欄です。
「相手と同じ目線で聞く」
「その場にいなくても，大きな声で御挨拶する」
この２つの話しが載っていて，その最後に次のように記されています。
何よりも，気をつけたいのものが姿勢です。横山験也著『行儀作法の教科書』（岩波ジュニア新書）は，役に立ちます。
友達の先生の本に，自分の本が紹介されました。嬉しいですね。
この本には，信頼を勝ち取る１０の原則が載っています。
それに続いて，事例が７６も載っています。
事例は「子どもとの関わり」「学校生活の約束」から始まり，「授業参観」「保護者会」など行事的な項目，さらに「けんか・怪我」「不登校」「お金に絡む問題」などに分類されて出ています。
お金関係の所は，ちょっとおかしくなると大変なことになりやすいので，特に，読んでおいた方が良いです。かなり重要なことが書いてあります。
私が一番関心を高めたのは，この本の１０６ページです。
不登校になりつつあるお子さんの保護者から，校長先生が話しを聞いてくれたところです。
「宿題が多い」「先生がすぐに怒る」「授業がわからない」
この３つが原因と聞き出してくれた校長先生はさすがです。
さて，そこからどう対応をしたらよいかです。
宿題が関わる時間，怒りが関わる時間に比べて，授業は長いです。
この長時間関わる授業を分かりやすくすること，できれば，面白くて休んでいられないような授業を連日することができれば，何とかなるのが人の世です。
手っ取り早いのは，算数ソフトを毎時間，５分１０分でも使うことです。ノリノリで授業をすれば，毎日，朝の１時間目か２時間目が楽しみの時間になります。寝坊をしているわけにはいきません。
そんなことを思いつつ，最後まで楽しく読みました。
右の図をご覧下さい。
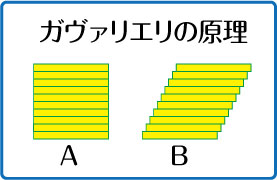
同じ長さの細長い板を１０枚ずつならべています。
Ａは真っ直ぐに並べていますが，Ｂはちょっとずつずらして並べています。
さて，どちらの面積の方が広いのでしょうか。
このように問われても，どちらかが広いとは思えません。広さは，重なってさえいなければ，並べ方によって左右されないからです。
ガリレオ（１５６４～１６４２）の高弟だった，１７世紀のイタリアの数学者ガヴァリエリ（１５９８～１６４７）は，それまでの数学の考えを進め，「面は幅のない線の集合」と考え『不可分量の幾何学』にまとめました。
この考え方は，頭が柔軟になります。Ａのカチッとした面積が自由自在に動き出すような気持ちになってくるからです。
ですので，『不可分量の幾何学』には，いったいどんな風に書いてあるのか気になります。読んでみたいと思うのですが，こういう本の翻訳本があるのかどうか，それすら分かりません。
今，小学校で教えている方法は，面積を辺でがっちり固定して見る方法です。ですので，見た通りにしか図形が見えてこない頭になっていきます。これは，教える先生も同じです。
これをガヴァリエリのように，積み重ねているという形でも扱うようになったら，高さが同じなら途中はどんな状態でも関係ないことがわかります。自由にスライドさせてもかまわないと頭が働くようになります。
こういうソフトを，いつかつくって，面積の発展的な見方として見てもらえたら良いなぁと思っています。しばらくは，作れませんが・・・。
