４年生の単元「変わり方」のソフトが１本，もうすぐできあがりそうです。
この単元のソフトは，「もっと！算数」に１本アップしているので，これで２本目となります。
１本目も，２本目のこのソフトも，力を入れているところは同じです。図の増減を見えるようにしています。
なにしろ，単元は「変わり方」です。どんな風に変わっていくのか，それを考える単元なのです。当然，変わる様子をしっかり見て，どう変わるかを考えるのが筋となります。
妙な話なのですが，算数は案外この「見る」部分がひ弱です。典型的なのは，「速さ」の学習です。速さを見ないまま，計算式を考えます。理科だったらあり得ない授業展開です。
このように言われても，実際のところ，算数の動きは，ちょっと見せづらいものがあります。ですので，これまでは，見せたくとも見せることが出来なったのです。これは致し方のないことです。でも，その代償は「落ちこぼれ」となって現れていました。悲しい現実です。この悲しみが昔話になるような時代へと，算数の授業を高めていく必要があります。
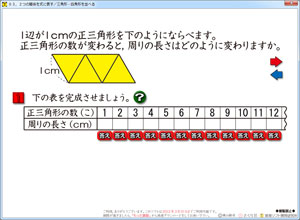
さて，上のソフトですが，画面の右に「→」「←」のボタンがありますね。これをクリックすると，三角形が増えたり，減ったりします。これだけで，ぐっと授業がしやすくなります。
問題１では，表づくりが出来ます。
表の中を３つぐらい作ると，「変わり方の規則性」に，うすうす気づいてきます。ここも重要です。算数は，この規則性に気づく瞬間を，子ども達に体感させることです。優秀な子が１人気がついて，発表して，それを聞いて気がつくより，気づきに多少の時間差を生じつつも，次々に「あっ，わかった！」と規則性に気づいていく事が大切です。
それをどうやるかは，算数ソフトを使った授業実践を体験することでつかんでください。
「変わり方」の２本目が完成したら，アップしていきます。
－－－－－－
算数のソフトは，さくら社から『子どもが夢中で手を挙げる算数の授業』という全３０巻の本になって発売されています。「もっと！算数」のサイトは，この本が出来た後に作られたソフトで構成されています。ですので，ベストの使い方は，本のソフトを補完する形で，もっと算数サイトのソフトを活用することとなります。
２年生の「１０００までの数」の学習に，数直線が出てきます。右のソフトは，その数直線の場面で活用するソフトです。
数直線ですから，「目盛りを読めるようにすれば良いのよ」と思われがちです。でも，これでは算数の豊かさが伝わりません。
もっとも大切なことは，「数直線が，０から指定の目盛りまでの量を表している」と認識出来るようにすることです。
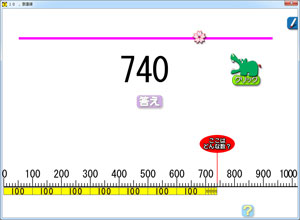
右の画面では，赤い線が「３４０」を指しています。そして，数直線の下に「１００束」「１０束」が登場しています。この「１００束」「１０束」の図が，「半具体図」です。
この図ですが，テープ図でも良いのですが，テープ図は長さだけで示す量の図ですので，「なぜ３２０なのか」を自然と理解させる力は持っていません。
半具体図になると，テープ図を１００単位，１０単位で区切ったスタイルになっているので，３２０になる意味がとてもわかりやすくなります。わかりやすいが故に，子どもが「ああ，そうか！」と，自分から納得する状態を作り出しやすくなります。能動的な状態です。ソフトを使うだけで，こうした能動的な脳の働きが得られます。
算数ソフトを使って算数の授業をされる先生がどんどん増えていますので，「半具体図」が数直線に付随する授業が全国で展開されることになります。算数の一つ一つをしっかり理解することにより，算数はおもしろい！と感じ取れる子が一人でも多く増えてくれたらと願っています。
このソフトは，『子どもが夢中で手を挙げる算数の授業』の２年３巻に収録されています。
算数ソフトですから，クリックすると問題が一瞬で変わります。同時に，半具体図も問題に応じて変わって行きます。何回も何回も半具体図を見ることが出来るので，自然と数直線に対する認識が豊かになっていきます。
総務省のＩＣＴ絆プロジェクトの会議があり，埼玉県の毛呂山町へ行ってきました。ipadが児童用として配置され，しかも，ウィンドーズへのリモートコントロールができるので，サーバーのソフトが自由に使える環境になります。今月中に配備完了となるそうです。新しい時代に向かって日本の教育が動き出していることを感じます。
毛呂山町の教育室長さんはＩＣＴについて実に博識で，ご自身でソフトを作り上げていることもありますが，マウスパッドも開発されています。世の中は広いと感じさせてくれる方です。
この総務省のプロジェクトは，１０月公募で１２月末に決定。それから一気にシステム設計，ハード設置，ソフト採択などがすすみ，３月末には完備です。猛スピードで動いています。ソフト採択では現場の先生方にソフト見ていただき，どれがよいか選定し，決定されました。担当した先生の作られた資料を拝見し，１行１行の裏に大変な時間と労力と学校の子ども達・現場の先生方への心配りがあることがわかり，胸にぐっと来ました。同様に，このプロジェクトと請け負ったキーウエアさんも短期間に困難なことをやってのけ，こちらも胸に詰まるものを感じます。こういう準備推進の皆さんの汗で新しい教育を押し開こうとしています。そこに関われたことをとても光栄に思っています。
正六角形の作図。
一通り，６分割の線が引けると，直線が順を追って登場してきます。
正六角形ができあがると，次へ進む事ができます。
次へ進むと，中に出来ている三角形が何であるか考える場面になります。正三角形だとわかったら，再び作図に戻り，どうして，半径で円周を６分割すると正六角形が描けるのか，考えてもらいます。理解が深まります。
火曜日には，「もっと！算数」サイトにアップできる予定でいます。
正六角形の作図ソフトがほぼ完成しました。
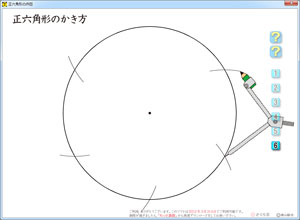
今，ちょっと気になっているのが，コンパスが透けていることです。どうして，透けてしまったのか，後で調べてみたいと思いますが，ソフトではこういった半透明も作り出せるので，なかなか面白いです。
作図は「実技」です。ですから，実際にどうやるかを見て学ぶことが大切です。黒板で先生のされる実際の作図。それをフォローするようにこのソフトが活用できます。
作図ソフトは，『子どもが夢中で手を挙げる算数の授業』にも収録されています。垂直線や平行線を作図するソフトが収録されています。
これを使った先生から，
「とても良かった」
「何度も繰り返し見せられるので，子どもたちもすぐに覚えてしまう」
など，うれしい声をいただいています。
何度もお手軽に見せることができるので，子ども達の頭にスーッと入っていくのです。
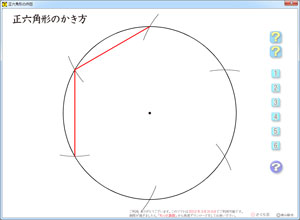
さて，この「正六角形の作図」ですが，次のようになっています。
－－
まず，円がスーッと描かれます。
次に，その円周をコンパスで６分割。１クリックで１分割が表示できるようにしています。
そうして，線がパッパッと出てきて，完成です。
－－
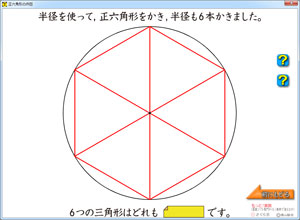
その後，内部の三角形がどんな三角形なのか学ぶコーナーが登場します。
近々，「もっと！算数」にアップします。 http://www.mott3su.jp/
教育の古書が１冊届きました。旧制中学の受験本『基本算術書』（大正３年）です。
その初っぱなに書いてあるが，数字の書き方です。
字ノ傾キト幅ト長サト字ノ間ダトヲ揃ヘテ美シク正シク書クコトノ練習ガ大切デアル。
私が，驚くのは，中学受験をする段階でも，字を丁寧に書くよう促していることです。
文字なら，少々雑になっても前後の流れから，その字がおよそ何であるかを推測できます。しかし，数字はそうはいきません。雑に書くと，誤読をすることが多々あります。これは，年齢に関係が無く，急いで雑に書くと，誰の数字でも誤読されやすくなります。それではいけないので，折を見ては，「数字は丁寧に！」と指導する必要があります。
この当時は，ごらんのように斜体で数字を書いていました。自分の父も母もこのような数字を書いていました。子ども心に，「お父さんの字は綺麗だ。お母さんの字は綺麗だ」と思っていましたが，自分は普通の数字を書いていました。
この数字。実にすごい世界を表しています。
文字の「あ」や「の」などは，集まって単語になるとあれこれ彷彿させてくれるのですが，バラされると，とっても無機質になります。
ところが，数字は「１」「５」とバラされていても，それなりの大きさを感じます。しかも，「リンゴが１こ」とか「山が１つ」などと，主語や単位がつくと，同じ１でも，ずいぶん大きさが違って感じます。それなのに，「１」は単なる１という大きさでしかなく，リンゴだろうが，山だろうが，個数としては１で同じなのです。「リンゴと山は同じなんだ！」なんて，ちょっとしたマジックのように感じられます。一対一対応の概念を持ってしまっているので，自然と同じなんだと見なせるのです。
さらに，「３５３」などと，単語のように数字が集まると，はじめの「３」と，最後の「３」では，意味が全く違ってきます。言葉の「とまと」は，はじめの「と」も，最後の「と」も，バラされてしまうと無機質で，何とも違いを感じ取れません。しかし，数は違って感じられてきます。れぞれの単位となっている大きさが違うからです。はじめの「３」の単位は「１００」。最後の「３」の単位は「１」です。こういったことを感じるのは，位取りという概念が体にしみこんでいるからです。
かの有名なヘーゲルは，数は「単位」であり，かつ「集合数」であると述べているそうです。でも，私にはヘーゲルのような大哲学者の考えることはよくわかりません。
ただ言えることは，数は丁寧に書かないと，こういう魔法のような世界が壊されてしまうと言うことです。
